
StickMan Physics
Animated Physics Lessons

Mechanical Energy Problem Solutions
Mechanical energy problems and solutions.
See examples of mechanical energy problems involving kinetic energy, potential energy, and the conservation of energy. Check your work with ours.
1. How much gravitational potential energy do you have when you lift a 15 N object 10 meters off the ground?

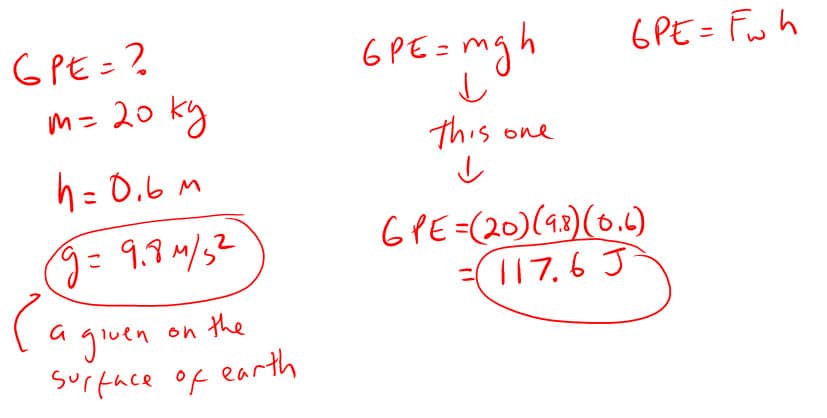
2. How much gravitational potential energy is in a 20 kg mass when 0.6 meters above the ground?
3. How much gravitational potential energy does a 35 kg boulder have when 30 meters off the ground?
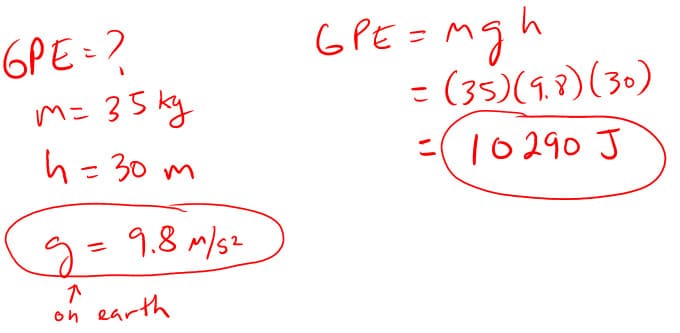
4. How many times greater is an objects potential energy when three times higher?
If you need help on ratio problems click the link below:
Rule of Ones: analyzing equations to determine how other variables change
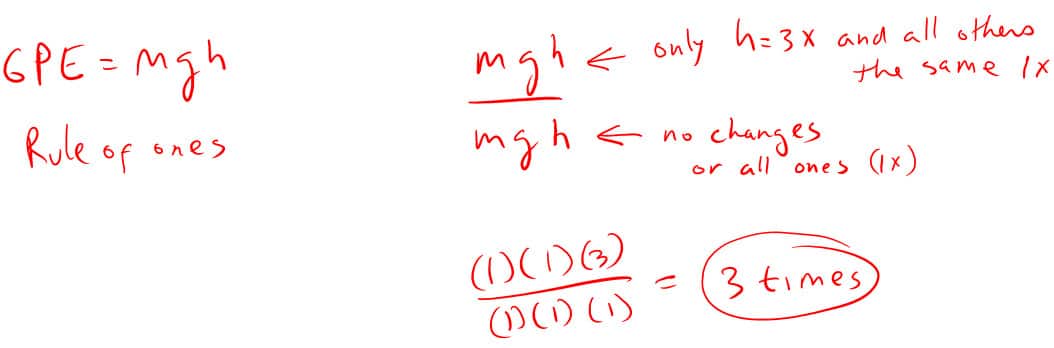
5. How much kinetic energy does a 0.15 kg ball thrown at 24 m/s have?
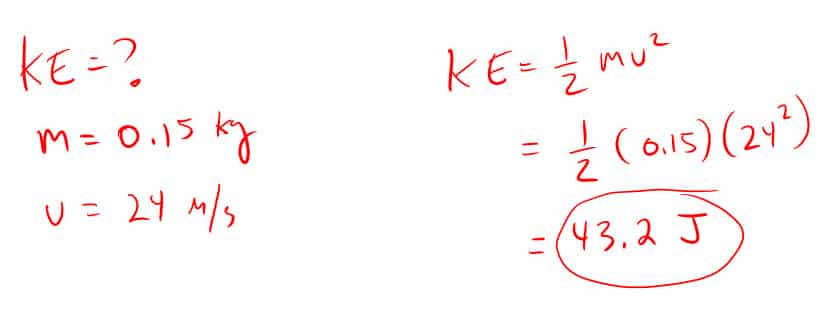
6. How many times greater is the kinetic energy of a ball that is going five times faster?
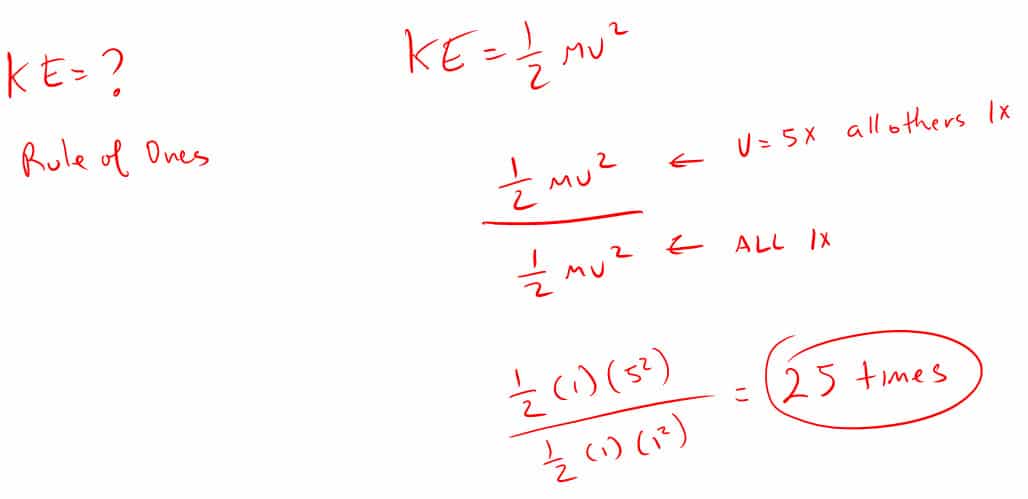
7. How much kinetic energy does a 1.2 kg ball have the moment it hits the ground 3.5 meters below when it starts from rest?
I cancelled out the initial kinetic energy because:
- KE i = ½ mv f 2
- KE i = (½)(3.5)(0 2 ) = 0 J
I cancelled out the final potential energy because:
- PE f = mgh f
- PE f = (3.5)(9.8)(0) = 0 J
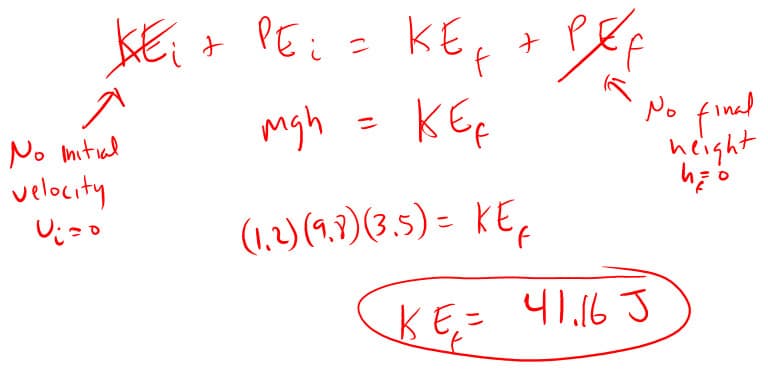
8. How fast is a 1.2 kg ball traveling the moment it hits the ground 3.5 meters below when it starts from rest?
(Note: In many of these problems I could cancel out mass but did not since it was provided)
Since I did not cancel out mass I could answer the following questions if asked:
- How much mechanical energy did you have at the beginning? (41.6 J)
- How much kinetic energy did you have at the beginning? (0 J)
- How much potential energy did you have at the beginning? (41.6 J)
- How much potential energy do you have at the end? (0 J)
If I cancelled out mass in my work it would not show the actual initial potential energy since PE i = mgh and not just gh.
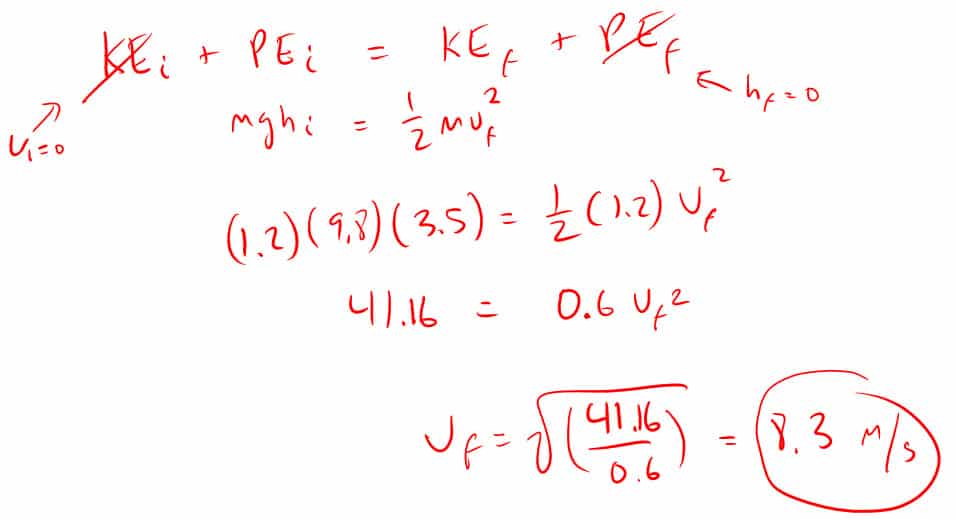
9. A 3.5 kg ball fell from a height of 12 meters. How fast is it traveling when its still 5 meters off the ground?
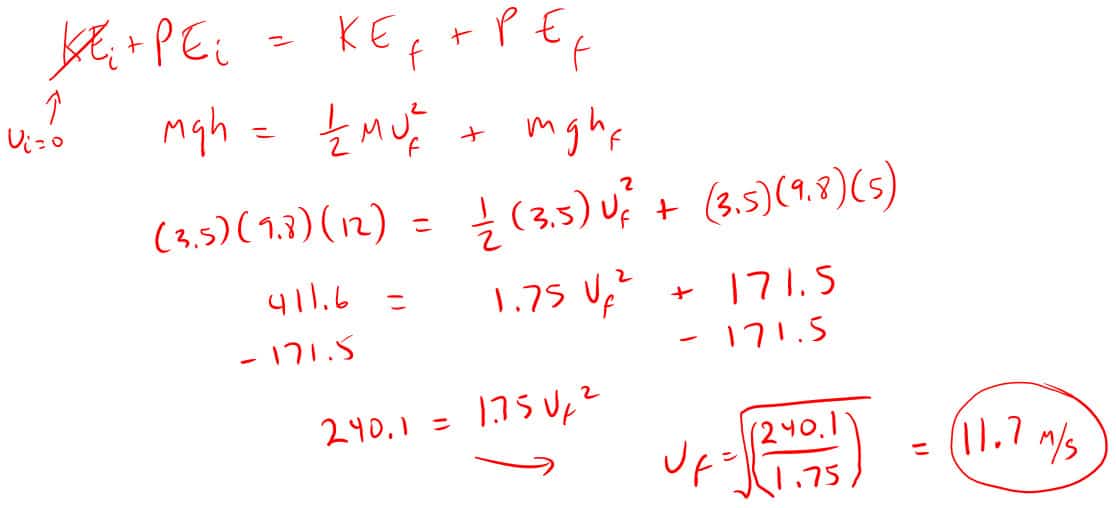
10. An 85kg roller coaster cart is traveling 4 m/s at the top of a hill 50 meters off the ground. How fast is it traveling at top of a second hill 20 meters off the ground?
- Back to the Mechanical Energy Page
- Back to the Main Work, Power, Mechanical Energy, and Simple Machines Page
- Back to the Stickman Physics Home Page
- For video tutorials and other physics resources check out HoldensClass.com
- Find many of your animation resources in one place at the StickMan Physics Gallery
- Equation Sheet
Terms and Conditions - Privacy Policy
- Total mechanical energy is just the kinetic plus potential energy.
- As long as there are no outside forces unaccounted for, we know that the totals before and after will be equal.
E k + E p = E k ’ + E p ’
Note: the little ’ just means “after”.
We usually call this the Law of Conservation of Energy . It grows out of the Laws of Thermodynamics .
First Law of Thermodynamics
“Energy can not be created or destroyed, only changed from one form to another.”
- This just basically means that if one thing loses energy, something else must be gaining energy. The opposite is also true.
- In an ideal situation this transfer of energy would be perfect and complete, but when was the last time you remember our universe being perfect…? This leads us to the second law …
Second Law of Thermodynamics
“In any energy conversion, there will always be some waste energy released as heat into the surrounding environment.”
In the second law we recognize that the total energy is constant, it’s just that some of the energy is released as unusable heat.
- This energy naturally flows from a hotter source to the cooler environment.
In most of the work we do, we assume that we are living in a “perfect” universe.
- This means that for the most part we will obey the first law, but ignore the second.
- There will be some situations when we give you enough information to use the second law, but we will be pretty specific about telling you.
- Most of the time we will say something about the friction involved, since this is the most common source for heat loss in your problems
Example 1 : A person is sitting on a toboggan at the top of a 23.7m tall hill. If the person and toboggan have a total mass of 37.3 kg determine how fast they will be going when they reach the bottom of the hill. Assume there is no friction.
At the top of the hill the person isn’t moving, so E k will be zero. At the bottom of the hill the E p will be zero. E k + E p = E k ’ + E p ’ ½ mv 2 + mgh = ½ mv’ 2 + mgh’ 0 + (37.3kg) (9.81m/s 2 ) (23.7m) = ½ (37.3kg) v’ 2 + 0 8.67e3 J = 18.7 v’ 2 v’ = 21.6 m/s
Notice how in this example all of the potential energy the object had at the top of the hill has been turned completely into kinetic energy at the bottom.
- It’s also possible to analyze how the potential energy steadily changes into kinetic energy during a fall…
Example 2 : Wile E. Coyote is trying to drop a boulder off a cliff to hit the Roadrunner eating a bowl of birdseed. He wants to know the speed of the boulder at various points. He supplies you with the following blueprint…
The Coyote wants you to determine the velocity of the boulder at several different heights above the ground, assuming no air resistance…
a) 45 m b) 30 m c) 10 m d) 0 m a) Well, this one ain’t so tough! Since it’s sitting at the top of the cliff, its velocity is 0 m/s. It might be handy at this point to calculate how much E p the boulder has. E p = mgh = 200kg (9.81m/s 2 ) (45m) = 88290 J = 8.8e4 J TOTAL ENERGY = 8.8e4 J
b) First, ask yourself how much E p the boulder still has at 30m above the ground.
E p = mgh = 200kg (9.81m/s 2 ) (30m) = 58860 J = 5.9e4 J
That means that 8.8e4 J - 5.9e4 J = 2.9e4 J is missing, right?
Wrong! According to the conservation of energy, that energy must now be kinetic !
TOTAL ENERGY = 8.8e4 J
c) Again, calculate how much E p you have at this new height of 10 m…
E p = mgh = 200kg (9.81m/s2) (10m) = 19620 J = 2.0e4 J
That means that I have changed 6.9e4 J of energy into other forms… we’ll assume it all changed into kinetic energy.
d) By the time the boulder has reached the ground, all of its potential energy is gone (it’s zero metres above the ground!). We all know that when it actually hits the ground it will come to rest, but we are concerned with how fast it’s going when it is right at ground level but hasn’t actually touched the ground yet. We can assume that all of the potential energy the boulder had at the top is now kinetic energy at the bottom…
You could be finding the same answers based on kinematics formulas from Physics 20.
- In fact, you’ll find that conservation of energy gives you new ways to do many problems that you did with kinematics formulas…
JEE-IIT-NCERT Physics & Math
Widget atas posting, conservation of mechanical energy problems and solutions.
| Fig.1 |
| Fig.2 |
| Fig.3 |
| Fig.4 |
| Fig.5 |
| Fig.6 |
| Fig.7 |
| Fig.8 |
| Fig.9 |
Post a Comment for "Conservation of Mechanical Energy Problems and Solutions"
Mechanical energy – problems and solutions
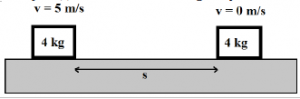
Mass of block (m) = 4 kg
Final velocity (v 2 ) = 0 m/s
f k d = ME 2 – ME 1
Work done by the kinetic friction force :
The kinetic energy of object B :
Because m g h = ½ m v 2 then we can change m g h in equation 1 with ½ m v 2 .
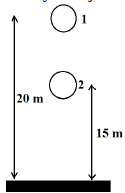
ME o = ME t
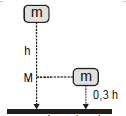
KE M = PE = m g (0.7 h)
6. If PE Q and KE Q have the potential energy and the kinetic energy at point Q (g = 10 m/s 2 ), then PE Q : KE Q =…

The ratio of the gravitational potential energy to the kinetic energy at point Q :
Share this:
Reset password New user? Sign up
Existing user? Log in
Conservation of Energy
Already have an account? Log in here.
- Shabarish Ch
- Kishore S. Shenoy
- Aakash Khandelwal
- Shubhang Sharma
- Josh Silverman
Some of the great tools in physics are so-called "conservation laws" that buttress the laws of motion with certain quantities that remain the same throughout time. Among these great laws is the conservation of energy which states that while energy can change forms, it cannot be created or destroyed.
Here we'll explore the partition between kinetic energy and potential energy, and how energy can in some sense replace forces in our calculations. We conclude with the introduction of formal methods of physics that analyze the dynamic behavior of systems solely in terms of energy, thus replacing the necessity of having to analyze forces at all. Such methods play a dominant role in systems of condensed matter, quantum field theory, and other problems far beyond elementary classical mechanics.
The Conservation of Kinetic Energy
Work-energy theorem, work with potential energy, conservation of kinetic and potential energies, conservation of energy in general, hamiltonians, lagrangians, and noether's theorem, additional conservation of energy problems solving.
For a person riding a bicycle, their kinetic energy \(E\) is equal to the amount of heat that would be dissipated from the moment they pull the brake to the moment they come to rest. If they don't skid, most of this heat will go into heating the brake pad and the metal rim of the wheel. If they do skid, most of the heat will go to the rubber in the tire and to the road. Before they pull the break, this energy can be observed as the ongoing motion of the parts of the bicycle, i.e. the net forward movement of the bicycle and the spinning of the wheels.
There are other forms of energy that a particle can have such as gravitational potential energy, chemical potential energy, electrical potential energy, spring potential energy, et cetera, but the kinetic energy is the portion of an object's energy that is due explicitly to its ongoing motion. For a point particle of mass \(\delta m\), moving at speed \(v\), the kinetic energy is given by the formula \(\frac12 \delta mv^2\), and the kinetic energy of any extended object can be built up from this. If a moving object collides with another object, and there is no dissipation, (no heat is given off, no chemical bonds are rearranged, etc.) then the total kinetic energy of the objects after the collision must equal the kinetic energy of the moving object before the collision.
In Isaac Newton's Principia Mathematica , momentum is defined and is said to be conserved, but there is no mention of energy anywhere in his treatise. Newton was able to work out the elliptical orbits of planets without any reference to energy at all. However, if we start with the assumption that momentum is conserved, we can derive the conservation of kinetic energy, and thus obtain the structure that lay hidden from Newton in his own theory.
Colliding balls on a table Consider a ball of mass \( m_{1} \) moving with velocity \( v_{0} \) in the direction of a stationary ball of mass \( m_{2} \). Let the velocities of the balls after the collision be \( v_{a} \) and \( v_{b} ,\) respectively. Moreover, suppose the collision is elastic, i.e. the relative velocity of approach is equal and opposite to the relative velocity of separation, i.e. \(\dfrac{\Delta v_i}{\Delta v_f} = -1\). Therefore, along with the conservation of momentum, we have \[\begin{align} v_{0} &= v_{b} - v_{a} \\ \\ m_{1}v_{0} &= m_{1}v_{a} + m_{2}v_{b}. \end{align}\] Solving these two equations for \( v_a \) and \( v_b ,\) we find \[\begin{align} v_a &= \dfrac{m_1 - m_2}{m_1 + m_2}v_0 \\\\ v_b &= \dfrac{2m_1}{m_1 + m_2}v_0. \end{align}\] Let us now calculate the initial and final kinetic energies \(\big(\frac12 mv^2\) for each ball\(\big):\) \[\begin{align} \textrm{KE} _{i} &= \dfrac{1}{2}m_{1}v_{0}^2 \\\\ \textrm{KE} _{f} &= \dfrac{1}{2}m_{1}v_{a}^2 + \dfrac{1}{2}m_{2}v_{b}^2. \end{align}\] Using the values of \( v_a \) and \( v_b \) from above we find (after some tedious algebra) \[\textrm{KE} _{initial} = \textrm{KE} _{final} .\] Hence, the total kinetic energy is conserved in elastic collisions. What about during the collision? Imagine we have two identical balls speeding with equal but opposite velocities to a collision. For an instant, neither ball is moving. So where did the kinetic energy of the balls go during this instant? The collision of the balls is not instantaneous. For a short interval, the kinetic energy of the balls is stored as elastic potential energy, after which it is reallocated to restore the original kinetic energy of the balls. Elastic energy is the potential energy stored in a deformed body, as for example with the compression of an elastic spring. At all times, the combined kinetic and elastic potential energy of the balls is constant. For more information on elastic collisions, see Analyzing Elastic Collisions .
In the previous example, we saw that the conservation of energy falls out in elastic collisions. What about when an object is accelerated by a gravitational field? Without a detailed understanding of potential energy, can we identify quantities that exchange with kinetic energy? Below, we analyze an especially profitable example of a skier on a frictionless slope.
The inclined plane Under constant acceleration, an object travels a distance \(d\) in the time \(t = \sqrt{\frac{2d}{a}}\). For a skier on an inclined plane, this time is given by \(\sqrt{\frac{2d}{g\sin\theta}}\). Also, starting from rest at the top of the incline, the skier has speed \(v = at = g\sin\theta \sqrt{\frac{2d}{g\sin\theta}} = \sqrt{2g\sin\theta d}\) at the bottom of the incline. Consider the change in kinetic energy \(\frac12 mv^2\). At the top of the incline, this quantity is equal to zero, and at the bottom of the incline it's equal to \(mgd\sin\theta\). We notice that \(mgd\sin\theta\) is simply the strength of the gravitational force times the vertical distance through which the skier has descended. Further, we notice that the quantity \(\frac12 mv^2 + mg(h_0-h)\) is a constant throughout the course of the skier's motion, i.e. kinetic energy exchanges with the quantity \(mg\Delta h\). Evidently, by falling through the distance \(\Delta h\), the skier has picked up kinetic energy \(\text{KE} = mg\Delta h\). This suggests that \(mg\Delta h\) is equal to the gravitational potential energy of the skier, which can reallocate to the kinetic energy, based on the skier's vertical position.
Thus, we have stumbled upon a conservation relation between kinetic energy and the gravitational potential energy. As you might imagine, in this example, the conservation is imposed by the fact that the system follows Newton's second law \(F = \frac{dp}{dt}\).
In general, we'll see that energy conservation holds in countless other scenarios. Further, in all the centuries of careful experimentation, a violation has never been identified (in macroscopic systems). For this reason, the conservation of energy has been elevated to the status of a law, i.e. a principle that is expected to hold for all processes in the universe.
In plain English, work means to do something productive. In physics, work is said to be done if force acts to displace an object. For example, when you push a sled across the snow, or lift a bucket of water onto a ledge, or pump up the tire on your bicycle, you've done work. This idea is captured in the definition of work which is the applied force along the direction of displacement times the displacement. Mathematically, we can write
\[W=\int \vec F\cdot d\vec s = Fs\cos\theta, \]
where \(\theta\) is the angle between the force and displacement vectors.
As you might imagine, performing work on an object cannot only change its displacement but its kinetic energy as well. We return once more to the example of the skier on the slope to see how these ideas are related.
Work on the skier Recall our results from above regarding the skier on the slope. Now, consider the work \(F\cdot s\), where \(F\) is the force of gravity along the incline, and \(s\) is the distance traveled along the incline. With \(F = mg\sin\theta\) and \(s=d\), we find \(F\cdot s = mg\sin\theta d\). This is curious. In descending the slope, we showed that the skier gained an amount of kinetic energy \(mgd\sin\theta\) which is also equal to the product of the force that acted on the particle, and the distance over which the particle traveled. Moreover, if we were to pull the skier up the slope at constant velocity, he'd have gained potential energy in the amount \(mgd\sin\theta\). One might be tempted to hypothesize that work delivers energy to objects. Indeed, during his descent the gravitational field does work upon the skier to speed him toward Earth, and in pulling him up the hill, we do work against the gravitational field. Work against a field can always be recouped later and thus we say it is stored kinetic energy or, in other words, potential energy.
Mathematically, we've shown \(\vec{F}\cdot\vec{d} = \Delta \textrm{KE} +\Delta \textrm{PE}= \frac12mv_f^2-\frac12mv_i^2 + mg\left(h_f-h_i\right)\).
This suggests that the cumulative pull of the skier by gravity has given rise to the kinetic energy of the particle at the expense of his initial potential energy. Thus, we can either look at the exchange as work done on the skier by the gravitational field, or as a reallocation of potential energy to kinetic energy.
This relationship would be quite useful if it holds in general, but as yet, it is just a nice coincidence we've noticed in our calculation. Next we look to Newton's laws for a way to put it on firm ground.
Newton's laws: a basis for work According to the second law, we have the following relationship between changes in velocity and a net applied force (for simplicity we work in one dimension, though the result easily generalizes): \[\begin{align}F_\textrm{net}&=ma\\ &=m\frac{\Delta v}{\Delta t}.\end{align}\] Rearranging, we have \[\begin{align} F_\textrm{net} \Delta t &= m \Delta v \\ &= \Delta p.\end{align}\] Because \(\displaystyle\Delta x = v \Delta t\), we can write \(\displaystyle F_\textrm{net} \Delta x / v = m \Delta v\), or \[ F_\textrm{net} \Delta x = m v\Delta v. \] This relation shows that if the object is traveling with velocity \(v\) and it is pushed through some small distance \(\Delta x\) parallel to the force \(\displaystyle F_\textrm{net}\), it will pick up the additional velocity \(\displaystyle \Delta v = \frac{F_\textrm{net}\Delta x}{mv}\). In three dimensions, our result is \(\displaystyle \vec{F}_\textrm{net}\cdot\Delta\vec{x} = m\vec{v}\cdot\Delta\vec{v}\). This relation provides the basis for what we suspected above, that forces can do work to endow particles with kinetic energy. We can now exploit the relation to prove the work-kinetic energy theorem.
Relation between work and kinetic energy
Work-Kinetic Energy Theorem The net work (i.e. work minus work performed against any external fields) done by the force on an object is equal to its change in kinetic energy: \[\Delta \text{KE} = \int \vec F \cdot d\vec s.\]
Now think about the ways in which you can prove this theorem before you reveal the proof, try proving it yourself, and don't worry if you weren't able to crack it because most of the people can't do it in a single go.
Proof for Work-Energy Theorem
Proof 1 : If we add up all of the incremental pushes \(F_\textrm{net}\Delta s\) that the particle receives over the distance \(d\), we get \(F_\textrm{net}\sum \Delta s = F_\textrm{net}d\). However, we showed that \(F_\textrm{net}\Delta s = mv\Delta v\), so we have \(F_\textrm{net}d = m\sum v\Delta v\), a sum over the incremental increases in velocity. Let us now perform the sum of the \(mv\Delta v\). To start, when \(v\) is zero, \(mv\) is zero; at the end, it is equal to \(mv_f \). If we divide the increases up into \(n\) equal pieces, the velocity increases \(\Delta v\) are each given by \(\frac{1}{n}v_f\), which we can pull out of the sum so that the sum becomes \(\dfrac{v_f}{n}\sum v\). Suppose we divide the velocity increase over many moments so that \(n\) is large and the changes are small. Now, the sum of \(v\) from \(0\) to \(v_f\) in \(n\) equally sized chunks is simply \(v\) times the average value of \(v\) over the range: \[\sum\limits_{v=0}^{v_f} v= n\frac{v_f}{2}.\] Therefore, \(\sum mv\Delta v\) is equal to \[\dfrac{mv_f}{n}\sum\limits_{v=0}^{v_f}\Delta v = \frac{mv_f}{n}n\dfrac{v_f}{2} = \dfrac12 mv_f^2,\] which implies \(F_\textrm{net}d=\frac12 mv_f^2.\) This proves that if we act on an object of mass \(m\) with a force \(F_\textrm{net}\) over a distance \(d,\) it ends up with a kinetic energy \(\frac12 mv_f^2\), where the velocity \(v_f\) is given by \(\sqrt{2F_\textrm{net}d/m}\). \(_\square\) \[\] Proof 2 : We know \[W = \int \vec F \cdot d\vec s.\] Since \(\vec F =m \vec a=m\dfrac{d\vec v}{dt},\) it follows that \[\begin{align} W &= \int \vec F \cdot d\vec s \\ &=\int m\dfrac{d\vec v}{dt}\cdot d\vec s =\int\limits_{\vec {v_0}}^{\vec{v_f}}m\dfrac{d\vec s}{dt} d\vec v \\ &=m\int\limits_{\vec {v_0}}^{\vec{v_f}} \vec v \cdot d\vec v =\Delta \textrm{KE}, \end{align}\] which proves \(\Delta \textrm{KE} = W. \ _\square\)
Thus, a force acting on an object through a distance transfers energy to the object, and we call this quantity, \(W_\textrm{net} = \displaystyle\int \vec{F}\cdot d\vec{s}\), the work. In a frictionless system, the work is equal to the change in energy caused by the force:
\[W_\textrm{net} = \Delta \textrm{KE} + \Delta \textrm{PE}.\]
More generally, the work is equal to the change in energy plus whatever heat is dissipated to the environment.
Potential energy is a form of energy due to the configuration or position of an object in a field. It can be seen as a stored form on kinetic energy in that it can be converted to kinetic energy by allowing an object to relax its position or configuration in a field. For example, if we release an electric dipole previously restrained at an angle in an electric field, or drop a massive object in a gravitational field, potential energy is converted to movement through relaxation.
Dams contain massive amount of water stored at a considerable height. When this water is released, the gravitational potential energy is converted to kinetic energy and the water flows, which in turn spins the turbines to generate electricity which can be stored as electric potential energy in batteries. Thus the water which was stored at a height is used to generate electricity in a time of scarcity. Thus kinetic energy can be captured and stored in various forms of potential energy to be extracted later.
Gottfried Wilhelm Leibniz in 1676-1689 was the first to attempt a definition of kinetic energy, and noticed that for some mechanical systems it seemed to be conserved. But remarkably, it was a French mathematician, Emilie du Chatelet, who was the first to propose and derive the conservation of total kinetic and potential energy. She was aware of Isaac Newton's Principia Mathematica and undertook its translation into French, which she completed in 1749. During those years of translation, she included her derivation of the conservation law as a supplement to Newton's treatise. Soon afterwards, mathematicians Leonhard Euler and Joseph-Louis Lagrange went on to develop a mathematical formalism of classical mechanics, based on her works.
The Ball In this example, we see the interplay of kinetic and potential energies of a falling ball such that their sum is constant, when air resistance is ignored. Consider a ball of mass \( m \) falling from rest from a height \( H \) above the ground. Initially, since the ball is at rest its kinetic energy and potential energy, respectively, are \[\begin{array} &\textrm{KE}_i = 0, &\textrm{PE}_i = mgH. \end{array} \] Let \(v\) be the speed of the ball when it is at height \( h \) above the ground. From the second kinematic equation we have \( v^2 = 2g(H-h) \). Hence, the kinetic energy of the ball at height \( h \) is \[\textrm{KE}_h = \dfrac{1}{2}mv^2 = mg(H-h). \] From the expression of potential energy, the potential energy at height \( h \) is \[\textrm{PE}_h = mgh. \] Thus, the sum of energies is \(\textrm{KE}_h + \textrm{PE}_h = mgH \), which is the same as the initial sum of energies.
Spring With Oscillating Mass When an ideal spring is either compressed or stretched a distance \(x\) from the origin where the spring force \(=0\), the potential energy stored in the spring with a spring constant \(k\) \((\)which comes from using force to compress the spring against the spring force \(F=kx)\) is \[PE = \dfrac{1}{2}kx^2,\] while kinetic energy of the oscillating mass \(m\) moving at velocity \(v\) is \[KE = \dfrac{1}{2}mv^2,\] the sum of which is the total energy \(E\). \(\;\) Since total energy is conserved , \(E\) is a constant over time, so differentiating both sides by time \(t\), we have \[\dfrac { d }{ dt } E=0 =\dfrac {dx}{dt} \dfrac { d }{ dx } \left( \dfrac { 1 }{ 2 } k{ x }^{ 2 } \right) +\dfrac {dv}{dt} \dfrac { d }{ dv } \left( \dfrac { 1 }{ 2 } m{ v }^{ 2 } \right) \implies vkx+amv=0.\] Simplifying, we have \[ -kx = ma = F,\] which is Hooke's Law stating that the spring force exerted on mass \(m\) at any point is equal to \(-kx\), a linear function of the distance from the origin where the force \(= 0,\) in the direction towards the origin. This can be restated in terms of time \(t\) \[\dfrac { m }{ k } \dfrac { { d }^{ 2 }x }{ d{ t }^{ 2 } } +x =0,\] a \(2^{\text{nd}}\) order differential equation which has the solution, where \(b\) is a constant: \[x \left( t \right) =b\sin\left( \sqrt { \dfrac { k }{m } }\, t \right). \] Thus, the spring with oscillating mass has a period \(T,\) which is \[T=2\pi \sqrt { \dfrac { m }{ k } }. \]
The pendulum When a pendulum of massless arm length \(L\) with mass \(m\) at the end of it is at angle \(\theta\) from vertical, the gravitational potential energy is \[PE=mgh=mgL(1-\cos\theta), \] while the rotational kinetic energy of the mass \(m\) is \[KE=\dfrac { 1 }{ 2 } I{ { \omega }^{ 2 } }=\dfrac { 1 }{ 2 } m{ L }^{ 2 }{ \omega }^{ 2 },\] the sum of which is the total energy \(E\). \(\;\) Since total energy is conserved , \(E\) is a constant over time, so differentiating both sides with respect to time \(t\), we have \[\begin{align} \dfrac { d }{ dt } E&=0\\ \dfrac { d\theta }{ dt } \dfrac { d }{ d\theta } [mgL( 1-\cos\theta)] +\dfrac { d\omega }{ dt } \dfrac { d }{ d\omega } \left( \dfrac { 1 }{ 2 } m{ L }^{ 2 }{ \omega }^{ 2 } \right)&=0 \\ \dfrac { d\theta }{ dt } mgL\sin\theta +\dfrac { d\omega }{ dt } m{ L }^{ 2 }\omega &=0\\ \frac { d\theta }{ dt } mgL\sin\theta +\frac { { d }^{ 2 }\theta }{ d{ t }^{ 2 } } m{ L }^{ 2 }\frac { d\theta }{ dt }&=0 \\ \dfrac { L }{ g } \dfrac { { d }^{ 2 }\theta }{ d{ t }^{ 2 } } +\sin\theta &=0. \end{align}\] As an approximation for small \(\theta\), we have \[\dfrac { L }{ g } \dfrac { { d }^{ 2 }\theta }{ d{ t }^{ 2 } } +\theta =0,\] a \(2^{\text{nd}}\) order differential equation which has the solution, where \(b\) is a constant: \[\theta \left( t \right) =b\sin\left( \sqrt { \dfrac { g }{ L } }\, t \right). \] Thus, the simple pendulum, for small \(\theta\), has a period \(T\) which is dependent only on \(L\) and \(g:\) \[T=2\pi \sqrt { \dfrac { L }{ g } }. \] Or more generally, for small \(\theta\) but with a rotational inertia of \(I\) \[T=2\pi \sqrt { \dfrac { I }{ mgL } } ,\] where \(L\) is the distance from the pivot to the center of mass of the pendulum. Compare the equations of both spring oscillation and simple pendulum, and see how there's an analogy of Hooke's Law in the latter.
Throughout the first half of the \(19^\text{th}\) century, engineers realized that thermal heat was another form of energy, capable of mechanical work. By 1850, the law of conservation of energy was formally stated for the first time, as the first law of thermodynamics . In the last decades of the \(19^\text{th}\) century, Ludwig Boltzmann developed the statistical mechanics theory of heat and entropy, showing the equivalence of kinetic and thermal heat energies, based on the theory that matter was made of atoms. Over time, other forms of energy were recognized such as elastic, electromagnetic, chemical, and nuclear energies, and the law of conservation of energy was generalized to include all such forms of energies.
Firing an Inelastic Shell A tank fires a special hollow shell that has \(N\) neon atoms inside it, so cold (somewhere near absolute zero Kelvin) that relative to the shell the atoms are not moving. The shell has a velocity of \(680\) meters per second, and it slams into a dirt wall and suffers a 100% inelastic collision, where the shell comes to a dead stop. But the neon atoms continue to bounce around inside the shell at the same velocity. What is the temperature of the neon gas inside the shell, after the shell has come to a dead stop? Treat neon as an ideal gas, i.e. point-like particles with mass, and disregard the mass or size of the hollow shell. Neon atoms are \(20.1797\text{ amu},\) or \(\frac { 20.1797 }{ \text{mole} } \) grams, where \(1\text{ mole} = 6.022\times { 10 }^{ 23 }\). The kinetic energy of \(N\) neon atoms travelling at \(680\) meters per second is \[N\frac { 1 }{ 2 } m{ v }^{ 2 }=N\frac { 1 }{ 2 } \left( \frac { 20.1797 }{ 6.022\times { 10 }^{ 23 } } \frac { 1 }{ { 10 }^{ 3 } } \right) { \left( 680 \right) }^{ 2 }\text{ Joules}=N\left( 7.747\times { 10 }^{ -21 } \right)\text{ Joules}.\] Since total energy is conserved , the kinetic energy of the neon atoms has been converted into thermal heat energy. From statistical mechanics of ideal gases, we then have \[N\left( 7.747\times { 10 }^{ -23 } \right)\text{ Joules}=N\frac { 3 }{ 2 } kT \text{ Joules},\] where \(k=1.381\times { 10 }^{ -23 }\text{ Joules/Kelvin}\) is the Boltzmann Constant, and \(T\) is temperature in \(\text{Kelvin}\). From this, we have \[\left( 7.757\times { 10 }^{ -21 } \right) \frac { 2 }{ 3k } =374.088\text{ Kelvin},\] which is just above the boiling point of water. Note that this result does not depend on the number \(N\) of neon atoms so that there could be a gram of neon in the shell, or a single atom of neon. The temperature of an ideal gas depends solely on the mass of the atom and the average velocity of the atoms, is not a form of energy, and does not have the physical dimensions of energy, which thermal heat energy does.
The Rocket Rocket physics describes one kind of rocket that uses fuel as a stored form of chemical energy, which is released in the combustion chamber of the rocket to generate the thrust to propel it. As the fuel is used up, the mass of the rocket drops, while its velocity increases. Using the law of conservation of momentum , velocity of a rocket as a function of mass describes how the following rocket equation can be derived: \[\begin{align} v_f &= v_0 + u\log \frac{M_0}{M_f} , \end{align}\] where \(v_f\) and \(M_f\) are the final velocity and mass, respectively, \(v_0\) and \(M_0\) are the initial velocity and mass, respectively, and \(u\) is the velocity of the rocket exhaust relative to the rocket. \[\text{Indian Polar Satellite Launch Vehicle XL which uses HTPB propellant}\] We can use the law of conservation of energy to derive the same result as follows: Let \(M_0-m\) be the rocket’s mass, where \(m\) is the consumed mass of fuel. Also, let \(v(m)\) be the velocity of the rocket as a function of \(m\), and \(u\) the velocity of the exhaust relative to the rocket. Then we have the following as the total energy of the rocket/exhaust gas system: \[E=\displaystyle \int _{ 0 }^{ m }{ \dfrac { 1 }{ 2 } } \big[ u-v\left( m \right) \big]^2\, dm+\dfrac { 1 }{ 2 } \left( { M }_{ 0 }-m \right) \big[v(m)\big]^2+{ PE }_{ \text{Fuel} }\left( { M }_{ 0 }-m \right), \] where the first term is the kinetic energy of the rocket exhaust gas, the second term is the kinetic energy of the rocket, and the last term \({ PE }_{\text{Fuel} }\left( { M }_{ 0 }-m \right) \) is the potential energy contained in the unburned fuel. The kinetic potential energy of this fuel when it is converted into exhaust gas is simply the kinetic energy it has at velocity \(u\), so we can rewrite this equation as \[E=\displaystyle \int _{ 0 }^{ m }{ \dfrac { 1 }{ 2 } } \big[u-v(m)\big]^2 \, dm+\dfrac { 1 }{ 2 } \left( { M }_{ 0 }-m \right) \big[v(m)\big]^2+\dfrac { 1 }{ 2 } \left( { M }_{ 0 }-m \right) { u }^{ 2 }.\] Since total energy is conserved , we can differentiate both sides by \(m\) with the result \[\begin{align} \dfrac { dE }{ dm } &=0\\\\ \dfrac { 1 }{ 2 }\big[u-v(m)\big]^2-\dfrac { 1 }{ 2 }\big[v(m)\big]^2-\left( {M}_ {0}-m \right) v\left( m \right) \dfrac { dv }{ dm } -\dfrac { 1 }{ 2 } { u }^{ 2 }&=0\\\\ -u-\left( {M}_ {0}-m \right) { \dfrac { dv }{ dm } }&=0\\\\ -\int _{ 0 }^{ m }{ \frac { u }{ {M}_ {0}-m } } \, dm&=\int dv \\\\ u\log\left( \dfrac { {M}_ {0 }}{ {M}_ {0}-m } \right) &={v}_{m}-{v}_{0}, \end{align}\] which agrees with the rocket equation given above. This equation is the most simplified form of rocket physics, which assumes that all the thrust is provided by the exhaust velocity of the combustion gases alone. A real rocket involves other considerations such as combustion gas pressure inside the nozzle.
Mass Energy in Nuclear Reactions A Deuterium atom, \(_1 ^2\ce{H}\), is an isotope of hydrogen that has a nucleus containing one proton and one neutron. Two of them, if collided together at a sufficiently high speed to overcome the Coulomb barrier, can fuse and produce a helium-3 atom \(\left(_2 ^3\ce{He}\right)\) and a free neutron \(\left(_0 ^1\ce{n}\right)\). \(_2 ^3\ce{He}\) is an isotope of helium that has two protons but only one neutron. Excess energy is produced from this fusion, which is carried away as kinetic energy in the products. In atomic mass units \((\text{amu})\), the masses of the nuclei are \[\begin{array}{llll} _1 ^2\ce{H}&=&2.01410179 &\text{ (amu)}\\ _2 ^3\ce{He}&=&3.0160293 &\text{ (amu)}\\ _0 ^1\ce{n}&=&1.008664916 &\text{ (amu)}. \end{array}\] Per Einstein’s \(E=m{ c }^{ 2 }\), mass-to-energy conversion from \(\text{amu}\) to million electron Volts is \[1\text{ amu} = 941.494\text{ MeV}.\] Now, calculate the energy \(E\) in \(\text{MeV}\), produced as the result of the following Deuterium+Deuterium fusion reaction: \[_{ 1 } ^{ 2 }\ce{H} + \ _{ 1 } ^{ 2 }\ce{H} \to \ _{ 2 }^{ 3 }\ce{He}+ \ _0^1\ce{n}+{ E }_{ \text{MeV} }.\] Two deuterium nuclei have a total mass of \(4.02820358\text{ amu},\) but the total mass of \(_2 ^3\ce{He}\) and \(_0 ^1\ce{n}\) is \(4.024694216\text{ amu},\) which is less. The theory of relativity says mass is another form of energy, so since total energy is conserved that missing \(0.00350936\text{ amu}\) mass was converted into energy. Using the mass-to-\(\text{MeV}\) conversion, this works out to about \(E=3.26895\text{ MeV}.\) Note: \(\text{eV}\), or electron volt, is not to be confused with \(\text{V}\), or volt. \(\text{eV}\) has dimensions of energy, or joules, while \(\text{V}\) is joules divided by charge.
If the energy produced is carried away by the products, and if both kinetic energy and momentum are conserved, what is the kinetic energy of the neutron after this fusion reaction? (Disregard the initial kinetic energies of the reactant Deuterium nuclei.) The conservation equations are \[\begin{align} \dfrac { 1 }{ 2 } m_{(^3\ce{He})} v_{(^3\ce{He})}^2+\dfrac { 1 }{ 2 } m_n v_n^2&=E\\ { m }_{ (^3\ce{He}) }{ { v }_{ (^3\ce{He}) } }+{ m }_{ n }{ { v }_{ n } }&=0. \end{align}\] Letting \({ E }_{(^3\ce{He} ) } \) and \({ E }_{ n }\) be the kinetic energies of the products resulting from the fusion, we can restate the two equations from both conservation laws as follows: \[\begin{align} { E }_{ (^3\ce{He}) }+{ E }_{ n }&=E\\ { E }_{(^3\ce{He})}{ m }_{ (^3\ce{He}) }&={ E }_{ n }{ m }_{ n }. \end{align}\] From these, we can work out the kinetic energy of the neutron \[{ E }_{ n }=\dfrac { { m }_{ (^3\ce{He}) } }{ { m }_{ (^3\ce{He}) }+{ m }_{ n } } E,\] which works out to approximately \(2.44969\text{ MeV}\) or \(2.450\text{ MeV}\), which is the usual published value.
ATP synthase, a molecular motor
Spring Pendulum: A Preview of Lagrangian Mechanics Examples given above included a pendulum in a gravitational field, and an oscillating spring-mass system. What if we were to combine them? A massless pendulum arm of relaxed length \(L\) is capable of stretching or compressing lengthwise, and a mass \(m\) is attached to the end of it. Then the position of the mass can be described by two functions to be determined: \[\begin{align} \text{Distance from pivot point } &=L+x(t) \\ \text{Angle from vertical } &=\theta(t). \end{align}\] The total kinetic energy is then the sum of radial and tangential components \[T=\dfrac { 1 }{ 2 } m { \left( \dfrac { dx }{ dt } \right) }^{ 2 }+\dfrac { 1 }{ 2 } m { \left( (L+x)\dfrac { d\theta }{ dt } \right) }^{ 2 } \] and the total potential energy is the sum of gravitational and spring potentials \[V=V\left(x,\theta\right)=-mg(L+x)\cos \theta +\dfrac { 1 }{ 2 } k{ x }^{ 2 },\] where \(g\) is the gravitational acceleration and \(k\) is the spring constant. There are two approaches to classical mechanics (see Lagrangian formulation of mechanics ), which can be briefly summarized as follows: \[\begin{array}{rl} \text{Hamiltonian:} &\mathcal{H} = T+V\\ \text{Lagrangian:} &\mathcal{L}=T-V, \end{array}\] which can be shown to be equivalent through the Legendre transform. In this exercise, we express this spring pendulum by its Lagrangian as follows: \[\mathcal{L}=T-V= \dfrac { 1 }{ 2 } m{ { \dot { x } }^{ 2 }+ \dfrac { 1 }{ 2 } m { \left( (L+x) \dot {\theta } \right) }^{ 2 } }+mg(L+x)\cos \theta -\dfrac { 1 }{ 2 } k{ x }^{ 2 }.\] The two Euler-Lagrange equations for these are then \[\begin{align} \dfrac { d }{ dt } \left( \dfrac { \partial \mathcal {L} }{ \partial \dot { x } } \right) &=\dfrac { \partial \mathcal {L} }{ \partial x } \implies m\ddot { x } =m(L+x){ \dot { \theta } }^{ 2 }+mg\cos \theta –kx\\ \dfrac { d }{ dt } \left( \dfrac { \partial \mathcal {L} }{ \partial \dot { \theta } } \right) &=\dfrac { \partial \mathcal {L} }{ \partial \theta } \implies m(L+x)\ddot { \theta } +2m\dot { x } \dot { \theta } =-mg\sin\theta. \end{align}\] The first is the radial force along the length of the pendulum arm while the second is the tangential force. The complete solution to this pair of differential equations is beyond the scope here, but this example is given to illustrate the generalized utility of treating problems of classical mechanics through the use of kinetic and potential energies, rather than the use of forces and momenta.
The LC Circuit: Via the Lagrangian Approach The classic LC circuit, in the simplest form, consists of an inductor and a capacitor, both of which are capable of storing energy: one electromagnetic and the other electrostatic. This circuit can be analyzed using Kirchhoff’s laws, which is the conventional approach. However, to demonstrate the power of the Lagrangian method, which treats energy as a generalized abstract quantity, the following is a way how the LC circuit can be analyzed in terms of energies alone: Let \(q\left(t\right)\) be the charge as a function of time \(t\). Also, let \(L\) be the inductance of the inductor, and \(C\) the capacitance of the capacitor. Then we can make the analogy of kinetic and potential energies as follows: \[\begin{align} T&=\dfrac { 1 }{ 2 } L{ \left( \dfrac { dq }{ dt } \right) }^{ 2 }\\ V&=\dfrac { 1 }{ 2C } { q }^{ 2 }. \end{align}\] The Lagrangian is then \[\mathcal{L}=\mathcal{L}\left( \dot { q } ,q \right) =T-V=\dfrac { 1 }{ 2 } L{ \dot { q } }^{ 2 }-\dfrac { 1 }{ 2C } { q }^{ 2 }.\] The Euler-Lagrange equation is then \[\dfrac { d }{ dt } \left( \dfrac { \mathcal{L} }{ \partial \dot { q } } \right) -\dfrac { \mathcal{L} }{ \partial q } =0\implies \ddot { q } +\dfrac { q }{ LC } =0,\] which yields the same solution as can be found by using Kirchhoff’s laws \[q\left( t \right) ={ q }_{ 0 }\cos\left( \omega t \right) \] given that \(q\left(0\right)=0, \dot{q}\left(0\right)=0\) and \(\omega =\frac { 1 }{ \sqrt { LC } } .\)
The total mechanical (kinetic + potential) energy of a free falling object are always equal to the potential energy at the height from which it was dropped from rest. Is this statement true or false?
Neglect air resistance.
An object is dropped from rest from a height of \(h\). What is the velocity of the object in the middle of its journey, i.e. when the object is at half its original distance to its destination?
Two bodies \(A\) and \(B\) have an equal momentum. But the mass of \(A\) is less than the mass of \(B\).
Which of the two will have more kinetic energy?
This problem is posted in connection to the upcoming collaboration party hosted by me! Interested people may come forward (just ping me on slack).
Problem Loading...
Note Loading...
Set Loading...
8.3 Conservation of Energy
Learning objectives.
By the end of this section, you will be able to:
- Formulate the principle of conservation of mechanical energy, with or without the presence of non-conservative forces
- Use the conservation of mechanical energy to calculate various properties of simple systems
In this section, we elaborate and extend the result we derived in Potential Energy of a System , where we re-wrote the work-energy theorem in terms of the change in the kinetic and potential energies of a particle. This will lead us to a discussion of the important principle of the conservation of mechanical energy. As you continue to examine other topics in physics, in later chapters of this book, you will see how this conservation law is generalized to encompass other types of energy and energy transfers. The last section of this chapter provides a preview.
The terms ‘conserved quantity’ and ‘conservation law’ have specific, scientific meanings in physics, which are different from the everyday meanings associated with the use of these words. (The same comment is also true about the scientific and everyday uses of the word ‘work.’) In everyday usage, you could conserve water by not using it, or by using less of it, or by re-using it. Water is composed of molecules consisting of two atoms of hydrogen and one of oxygen. Bring these atoms together to form a molecule and you create water; dissociate the atoms in such a molecule and you destroy water. However, in scientific usage, a conserved quantity for a system stays constant, changes by a definite amount that is transferred to other systems, and/or is converted into other forms of that quantity. A conserved quantity, in the scientific sense, can be transformed, but not strictly created or destroyed. Thus, there is no physical law of conservation of water.
Systems with a Single Particle or Object
We first consider a system with a single particle or object. Returning to our development of Equation 8.2 , recall that we first separated all the forces acting on a particle into conservative and non-conservative types, and wrote the work done by each type of force as a separate term in the work-energy theorem. We then replaced the work done by the conservative forces by the change in the potential energy of the particle, combining it with the change in the particle’s kinetic energy to get Equation 8.2 . Now, we write this equation without the middle step and define the sum of the kinetic and potential energies, K + U = E ; K + U = E ; to be the mechanical energy of the particle.
Conservation of Energy
The mechanical energy E of a particle stays constant unless forces outside the system or non-conservative forces do work on it, in which case, the change in the mechanical energy is equal to the work done by the non-conservative forces:
This statement expresses the concept of energy conservation for a classical particle as long as there is no non-conservative work. Recall that a classical particle is just a point mass, is nonrelativistic, and obeys Newton’s laws of motion. In Relativity , we will see that conservation of energy still applies to a non-classical particle, but for that to happen, we have to make a slight adjustment to the definition of energy.
It is sometimes convenient to separate the case where the work done by non-conservative forces is zero, either because no such forces are assumed present, or, like the normal force, they do zero work when the motion is parallel to the surface. Then
In this case, the conservation of mechanical energy can be expressed as follows: The mechanical energy of a particle does not change if all the non-conservative forces that may act on it do no work. Understanding the concept of energy conservation is the important thing, not the particular equation you use to express it.
Problem-Solving Strategy
- Identify the body or bodies to be studied (the system). Often, in applications of the principle of mechanical energy conservation, we study more than one body at the same time.
- Identify all forces acting on the body or bodies.
- Determine whether each force that does work is conservative. If a non-conservative force (e.g., friction) is doing work, then mechanical energy is not conserved. The system must then be analyzed with non-conservative work, Equation 8.12 .
- For every conservative force that does work, choose a reference point and determine the potential energy function for the force. The reference points for the various potential energies do not have to be at the same location.
- If no non-conservative work is done, apply the principle of mechanical energy conservation by setting the sum of the kinetic energies and potential energies equal at every point of interest.
Example 8.7
Simple pendulum.
Since the particle is released from rest, the initial kinetic energy is zero. At the lowest point, we define the gravitational potential energy to be zero. Therefore our conservation of energy formula reduces to
The vertical height of the particle is not given directly in the problem. This can be solved for by using trigonometry and two givens: the length of the pendulum and the angle through which the particle is vertically pulled up. Looking at the diagram, the vertical dashed line is the length of the pendulum string. The vertical height is labeled h . The other partial length of the vertical string can be calculated with trigonometry. That piece is solved for by
Therefore, by looking at the two parts of the string, we can solve for the height h ,
We substitute this height into the previous expression solved for speed to calculate our result:
Significance
Check your understanding 8.7.
How high above the bottom of its arc is the particle in the simple pendulum above, when its speed is 0.81 m / s ? 0.81 m / s ?
Example 8.8
Air resistance on a falling object.
Step 2: Gravitational force is acting on the panel, as well as air resistance, which is stated in the problem.
Step 3: Gravitational force is conservative; however, the non-conservative force of air resistance does negative work on the falling panel, so we can use the conservation of mechanical energy, in the form expressed by Equation 8.12 , to find the energy dissipated. This energy is the magnitude of the work:
Step 4: The initial kinetic energy, at y i = 1 km , y i = 1 km , is zero. We set the gravitational potential energy to zero at ground level out of convenience.
Step 5: The non-conservative work is set equal to the energies to solve for the work dissipated by air resistance.
Check Your Understanding 8.8
You probably recall that, neglecting air resistance, if you throw a projectile straight up, the time it takes to reach its maximum height equals the time it takes to fall from the maximum height back to the starting height. Suppose you cannot neglect air resistance, as in Example 8.8 . Is the time the projectile takes to go up (a) greater than, (b) less than, or (c) equal to the time it takes to come back down? Explain.
In these examples, we were able to use conservation of energy to calculate the speed of a particle just at particular points in its motion. But the method of analyzing particle motion, starting from energy conservation, is more powerful than that. More advanced treatments of the theory of mechanics allow you to calculate the full time dependence of a particle’s motion, for a given potential energy. In fact, it is often the case that a better model for particle motion is provided by the form of its kinetic and potential energies, rather than an equation for force acting on it. (This is especially true for the quantum mechanical description of particles like electrons or atoms.)
We can illustrate some of the simplest features of this energy-based approach by considering a particle in one-dimensional motion, with potential energy U ( x ) and no non-conservative interactions present. Equation 8.12 and the definition of velocity require
Separate the variables x and t and integrate, from an initial time t = 0 t = 0 to an arbitrary time, to get
If you can do the integral in Equation 8.14 , then you can solve for x as a function of t .
Example 8.9
Constant acceleration.
Solving for the position, we obtain x ( t ) = x 0 − 1 2 ( E / m x 0 ) t 2 x ( t ) = x 0 − 1 2 ( E / m x 0 ) t 2 .
Check Your Understanding 8.9
What potential energy U ( x ) U ( x ) can you substitute in Equation 8.13 that will result in motion with constant velocity of 2 m/s for a particle of mass 1 kg and mechanical energy 1 J?
We will look at another more physically appropriate example of the use of Equation 8.13 after we have explored some further implications that can be drawn from the functional form of a particle’s potential energy.
Systems with Several Particles or Objects
Systems generally consist of more than one particle or object. However, the conservation of mechanical energy, in one of the forms in Equation 8.12 or Equation 8.13 , is a fundamental law of physics and applies to any system. You just have to include the kinetic and potential energies of all the particles, and the work done by all the non-conservative forces acting on them. Until you learn more about the dynamics of systems composed of many particles, in Linear Momentum and Collisions , Fixed-Axis Rotation , and Angular Momentum , it is better to postpone discussing the application of energy conservation to then.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Authors: William Moebs, Samuel J. Ling, Jeff Sanny
- Publisher/website: OpenStax
- Book title: University Physics Volume 1
- Publication date: Sep 19, 2016
- Location: Houston, Texas
- Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Section URL: https://openstax.org/books/university-physics-volume-1/pages/8-3-conservation-of-energy
© Jul 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- Intro Physics Homework Help
- Advanced Physics Homework Help
- Precalculus Homework Help
- Calculus Homework Help
- Bio/Chem Homework Help
- Engineering Homework Help
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
- Homework Help
- Introductory Physics Homework Help
Total Mechanical Energy Problem
- Thread starter Snape1830
- Start date Jan 15, 2012
- Tags Energy Mechanical Mechanical energy
- Jan 15, 2012
- Research team uses tunable laser to develop straightforward broadband spectroscopy method with Hz-level precision
- Scientists observe first neutrinos with prototype detector
- Chip that entangles four photons opens up possibility of inviolable quantum encryption
Without friction, total mechanical energy is a conserved quantity. What's the total mechanical energy at location A?
gneill said: Without friction, total mechanical energy is a conserved quantity. What's the total mechanical energy at location A?
Snape1830 said: PE= mgh. So PE= 17640 J Ohh I get it! So 17640=TME since kientic energy is 0 J. I completely forgot about that. Thanks!
- Jan 22, 2012
Hello, To calculate the total mechanical energy (TME) of the roller coaster at points B, C, and D, we first need to find the velocity at these points. We can use the principle of conservation of energy, which states that energy cannot be created or destroyed, only transferred from one form to another. At point A, the roller coaster has only potential energy (PE) as it is at rest. As it moves down the hill, this potential energy is converted into kinetic energy (KE). At point B, the roller coaster has lost some potential energy but gained some kinetic energy. We can use the equation PE = mgh (mass x gravity x height) to calculate the potential energy at point A. Since the velocity at the top of the hill is 0 m/s, the kinetic energy at point A is also 0. At point B, the roller coaster has lost 15 m of height, so the potential energy is now mgh = (120 kg)(9.8 m/s^2)(15 m) = 17,640 J. To find the velocity at point B, we can use the equation KE = 1/2mv^2 (1/2 x mass x velocity squared). We know the mass (120 kg) and the kinetic energy (17,640 J), so we can solve for the velocity: v = √(2KE/m) = √(2 x 17,640 J / 120 kg) = 14.7 m/s. We can use the same process to find the velocity at points C and D. At point C, the height has decreased by 12 m, so the potential energy is now mgh = (120 kg)(9.8 m/s^2)(12 m) = 11,520 J. The velocity can be found using the same equation as before: v = √(2KE/m) = √(2 x 11,520 J / 120 kg) = 12.3 m/s. At point D, the height has decreased by 8 m, so the potential energy is now mgh = (120 kg)(9.8 m/s^2)(8 m) = 9,600 J. Again, we can use the same equation to find the velocity: v = √(2KE/m) = √(2 x 9,600 J / 120 kg) = 10 m
Related to Total Mechanical Energy Problem
1. what is total mechanical energy.
Total mechanical energy is the sum of kinetic energy and potential energy in a system. It is a measure of the energy an object possesses due to its position and motion.
2. How is total mechanical energy calculated?
The total mechanical energy of a system is calculated by adding the kinetic energy, which is equal to 1/2mv^2, and the potential energy, which is equal to mgh, where m is the mass of the object, v is its velocity, g is the acceleration due to gravity, and h is the height of the object.
3. Is total mechanical energy conserved?
According to the law of conservation of energy, total mechanical energy is conserved in a closed system. This means that the total amount of energy in the system remains constant, even if it is transferred between different forms of energy such as kinetic and potential energy.
4. What happens to total mechanical energy when work is done on a system?
When work is done on a system, the total mechanical energy of the system will change. If work is done by a conservative force, such as gravity, the change in total mechanical energy will be equal to the work done. However, if work is done by a non-conservative force, such as friction, some of the mechanical energy will be converted into other forms of energy, such as heat.
5. How is total mechanical energy useful in solving problems?
Total mechanical energy is useful in solving problems because it allows us to analyze the motion of an object by considering its energy instead of individual forces. By using the conservation of energy principle, we can solve for unknown variables, such as velocity or height, without needing to know the specific forces acting on the object.
Similar threads
- Mar 13, 2021
- Jul 14, 2022
- May 10, 2024
- Nov 20, 2019
- Jun 30, 2024
- Jun 27, 2024
- Oct 30, 2022
- Apr 27, 2020
- May 7, 2023
- Sep 6, 2020
Hot Threads
- Current through a circuit when the key is open
- Small oscillations of a simple pendulum placed on a moving block
- How to Calculate Water Leakage in an Inverted Bottle Experiment?
- Vertical displacement with time of a projectile
- Acceleration in uniform circular motion is uniform or non-uniform?
Recent Insights
- Insights PBS Video Comment: “What If Physics IS NOT Describing Reality”
- Insights Aspects Behind the Concept of Dimension in Various Fields
- Insights Views On Complex Numbers
- Insights Addition of Velocities (Velocity Composition) in Special Relativity
- Insights Schrödinger’s Cat and the Qbit
- Insights The Slinky Drop Experiment Analysed
- New Hampshire
- North Carolina
- Pennsylvania
- West Virginia
- Online hoaxes
- Coronavirus
- Health Care
- Immigration
- Environment
- Foreign Policy
- Kamala Harris
- Donald Trump
- Mitch McConnell
- Hakeem Jeffries
- Ron DeSantis
- Tucker Carlson
- Sean Hannity
- Rachel Maddow
- PolitiFact Videos
- 2024 Elections
- Mostly True
- Mostly False
- Pants on Fire
- Biden Promise Tracker
- Trump-O-Meter
- Latest Promises
- Our Process
- Who pays for PolitiFact?
- Advertise with Us
- Suggest a Fact-check
- Corrections and Updates
- Newsletters
Stand up for the facts!
Our only agenda is to publish the truth so you can be an informed participant in democracy. We need your help.
I would like to contribute
Fact-checking donald trump’s rally in bozeman, montana.
- 2024 Senate Elections
Republican presidential nominee former President Donald Trump pauses to talk to onlookers after speaking at an Aug. 9, 2024, campaign rally in Bozeman, Montana. (AP)

In his first campaign rally since Vice President Kamala Harris selected Minnesota Gov. Tim Walz as her running mate for the 2024 presidential election, former President Donald Trump attacked Walz and rallied support for a crucial Senate seat in Montana.
"If Comrade Walz and Comrade Harris win this November, the people cheering will be the pink-haired Marxists, the looters, the perverts, the flag burners," Trump said, invoking a common but misleading line of attack that seeks to paint Democrats’ policies as socialist.
Trump took the stage later than expected at his Friday night rally in Bozeman, Montana, after a mechanical problem forced his plane to divert 140 miles east to Billings. The plane landed without incident. Trump’s vice presidential running mate, Ohio Sen. J.D. Vance, did not attend.
In his speech, Trump zeroed in on the state’s Democratic senator, Jon Tester, criticizing the votes Tester took to support major legislation passed under President Joe Biden’s administration, such as the Inflation Reduction Act. Tim Sheehy, the Republican running to unseat Tester, spoke alongside Trump.
Trump also criticized Harris and Biden on issues such as immigration and the economy. We fact-checked five of his claims.
Trump: I handed Biden "a surging economy with no inflation."
This is inaccurate . Trump has made this claim before.
Although inflation was lower during Trump’s presidency than it has been under Biden’s, the Consumer Price Index 12-month change was never at zero percent.
It fell close to zero in April and May 2020, shortly after the COVID-19 pandemic’s onset. The lowest inflation rate was 0.1% in May 2020.
That’s because the American economy took a major hit as the demand for goods and services plunged during the pandemic’s initial lockdowns. Trump claiming credit for the low inflation at that time ignores that the rate dropped because of economic crisis, not success.
For much of Trump’s presidency until the pandemic, inflation ranged from 1.5% to 3%. When Biden entered office in January 2021, inflation was at 1.4%.
Trump: "By the millions and millions, (immigrants are) coming from prisons, they’re coming from jails."
Pants on Fire!
Trump’s claim that immigrants are flowing across the border from prisons and mental institutions lacks evidence, and data and expert analysis reveal his description of them coming by the "millions and millions" to be so implausible as to be ridiculous.
U.S. Customs and Border Protection data shows that officials have arrested just more than 110,000 noncitizens with criminal convictions, whether in the U.S. or abroad. Not all were let into the country. The data reflects numbers the federal government knows about, but it isn’t exhaustive.
There have been about 8 million encounters at the border since Biden took office. But encounters data represents events, not people. For example, if one person tries to cross the border three times and is stopped each time, that would count as three encounters.
Trump: Harris "wants to get rid of ICE."
Harris was critical of the U.S. Immigrations and Customs Enforcement — the agency in charge of detaining and deporting immigrants who are in the U.S. illegally — during Trump’s presidency. She criticized many of his border policies, including one that led to family separations at the border, but she hasn’t called to abolish the agency.
She said in a 2018 MSNBC interview that Immigration and Customs Enforcement should exist, but she called for reexamining its role and scope. During a separate interview in 2018 , she said that the U.S. should "reexamine ICE and its role" and mission, and "even think about starting from scratch." Harris has not stumped in 2024 to end the agency; her campaign has not released a written policy platform for her 2024 run. But her 2019 presidential primary immigration platform called for restructuring the agency, not abolishing it.
Trump: "They're destroying Social Security and Medicare by allowing all of these people to come in on the plan."
Most immigrants in the country illegally are not eligible for Social Security. Some who have been granted humanitarian parole for more than one year may be eligible for Social Security for up to seven years, according to the Congressional Research Service.
Immigrants in the U.S. illegally are typically ineligible to enroll in federally funded health care programs such as Medicare and Medicaid. Some states offer Medicaid coverage under state-funded programs regardless of immigration status, and immigrants are eligible for emergency Medicaid regardless of status.
Immigration also does not threaten Social Security’s sustainability. The program has shortfalls because the ranks of retirees outpace the numbers of workers feeding their tax dollars into the system. Immigrants who meet the legal requirements to receive retirement benefits can access Social Security only after working and contributing to Social Security taxes for a minimum of 10 years.
Trump: Harris "wants to have all of your guns taken away."
Mostly False .
As presidential candidate in 2019, Harris said she supported a "mandatory gun buyback program" for assault weapons.
The proposed program did not apply to all guns. Handguns, which would not have been affected, make up the majority of guns sold in the U.S.
Since Harris has become the Democratic presidential nominee, her campaign has said she does not support a mandatory buyback program. The campaign said she supports banning assault weapons but not requiring people to sell them to the federal government.
Our Sources
Sources linked in article
Browse the Truth-O-Meter
More by caleb mccullough.

- Memberships
MoSCoW Method of Prioritization explained

MoSCoW Method: This article explains MoSCoW Method in a practical way. Next to what it is (meaning, acronym and origin), and which advantages are connected to using this model, this article also highlights the MoSCoW Method requirements, including a practical example. You will also learn how applying this method will enable you and the team to reach deadlines in time. Enjoy reading!
What is the MoSCoW Method of Prioritization?
Prioritising is often challenging. Particularly when it comes the implementation of new ideas and / or technologies. Everyone in an organisation always wants everything to be done right away and that is practically impossible. There are several tools available to make prioritisation easier. The MoSCoW Method of Prioritization is one them.
The MoSCoW Method is a prioritization technique, which can be used in a variety of situations.

Origin and advantages of the MoSCoW Method
The method was developed by Dai Clegg, a developer working for the software company Oracle .
Originally, it was used to categorize product features, derived from user stories. It was later used in the Dynamic System Development Method (DSDM) . The method contains multiple prioritization categories, with labels for each requirement, making it easier to prioritise.
Even though the origin of this prioritize method is in software development, it is also highly applicable for agile project management, market launches, product releases, starting a new business or change processes.
With the MoSCoW Method, requirements are determined for the result of the project or product. It is about setting requirements by order of priority. The most important requirements need to be met first for a greater chance of success.
Meaning and acronym of the MoSCoW Method
Moscow is an acronym made up of the first letters. The two Os have been added to make the word ‘moscow’ readable, they don’t have any meaning themselves. The M stands for ‘Must haves’ , S for ‘Should haves’ , C for ‘Could haves’ and W for ‘Won’t haves’ or ‘Would haves’ .
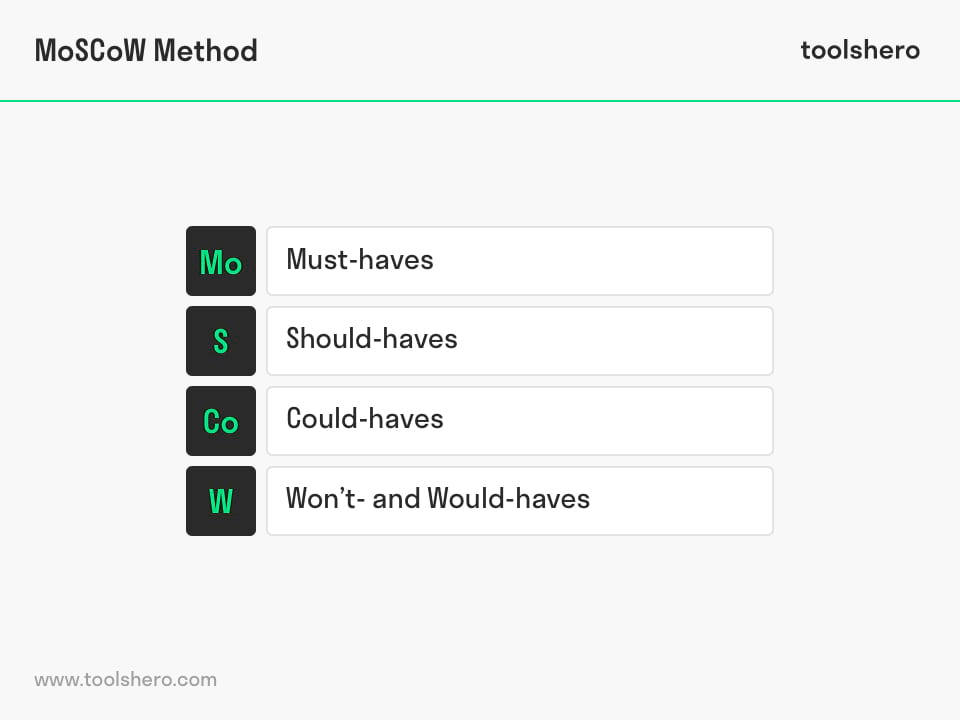
Figure 1 – the MoSCoW Method acronym
The requirements when you start with the MoSCoW Method
It’s a good idea to first specify the requirements together with all team members before starting the MoSCoW Method. When determining the requirements, you should take into account what is important to all the stakeholders. Brainstorming with everyone involved will lead to good, qualitative requirements.
The requirements are prioritised to prevent them from becoming to expensive or unrealistic. The main goal is to come up with requirements that add the most value for the company. The project requirements are divided into one of the following categories:
M – Must haves
These are about the minimal requirements that are determined in advance that the end-result has to meet.
Without meeting these requirements, the project fails and the product won’t be use-able. They are a necessity for a workable product and there is no alternative. The ‘Must haves’ are essential. MUST is also explained as an acronym that stands for Minimum Use-able SubseTs.
As an extra exam assignment, University of Applied Sciences Automotive students have been asked to design a car that can at least drive (minimal requirements).
It’s okay if the car only has a chassis, without any bodywork. It’s about the construction of the individual parts and drive train to the combustion engine. In this case, the Must have is that they have a drivable car by the end of the academic year.
S – Should haves
These are additional and much desired requirements that have a high priority, but are not essential for a usable end product. The product will be usable even if these requirements aren’t met. When they are met, they will only add to the value of the product. Depending on the available time, you can always return to these requirements at a later time.
The University of Applied Sciences Automotive student might like to add a tow bar to the car (should have), but as long as the car can drive without the tow bar, their project will be successful. They can always add the tow bar at a later stage.
C – Could haves
These requirements can be considered if there’s time left. If not, it’s no problem and will not have a negative effect on the final result. The ‘Could haves’ have a lower priority than the ‘Should haves’ .
This option will only be included if there really is more than enough time to make it work. This category is also referred to as ‘nice to have’; they’re more a wish than an absolute requirement.
The University of Applied Sciences Automotive students would perhaps like to install a tachometer in the car. It’s not an important (exam) requirement, but it’d be great if they manage to do it.
W – Won’t haves (and would haves)
These are about wishes for the future that are often impossible to realise or cost a lot of time. If it’s simply not possible, it’s best not to waste any energy on it.
If it is achievable, then a lot of time (and money) will have to be invested and it’s labelled a ‘Would have’. ‘Would haves’ are often followed upon at a later stage after the initial project is finished.
The University of Applied Sciences Automotive students don’t have to make a car that will actually drive on public roads.
It’s meant for study. If they do want to take it on public roads, it will need bodywork and comply with safety standards. It also involves getting approval from the Vehicle Standards Agency in elaborate process.
How to reach deadlines using the MoSCoW Method of Prioritization?
Correctly applying and sticking to the MoSCoW Method will lead to a clear way to lead a project. Everyone involved with the project will know what needs to be done first, when it has to be finished and why it’s important. By assigning priorities to requirements, a project becomes more manageable and it’ll be easier to meet the deadline.

It’s Your Turn
What do you think? How do you apply the MoSCoW analysis in your project or organisation? Do you recognize the practical explanation or do you have more additions? What are your success factors for applying the MoSCoW Method?
Share your experience and knowledge in the comments box below.
More information
- Baxter, R. (2004). Software engineering is software engineering . In 26th International Conference on Software Engineering, W36 Workshop Software Engineering for High Performance System (HPCS) Applications (pp. 4-18).
- Stephens, R. (2015). Beginning Software Engineering . Wrox Publishing .
- Hatton, S. (2008). Choosing the right prioritisation method. In Software Engineering, 2008. ASWEC 2008 . 19th Australian Conference on (pp. 517-526). IEEE.
- Robson, W.A., Simon, Shena. (2014). Moscow in the making . Taylor & Francis Ltd.
How to cite this article: Mulder, P. (2017). MoSCoW Method of Prioritization . Retrieved [insert date] from Toolshero: https://www.toolshero.com/project-management/moscow-method/
Original publication date: 05/12/2017 | Last update: 05/27/2024
Add a link to this page on your website: <a href=”https://www.toolshero.com/project-management/moscow-method/”> Toolshero: MoSCoW Method of Prioritization</a>
Did you find this article interesting?
Your rating is more than welcome or share this article via Social media!
Average rating 3.8 / 5. Vote count: 8
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you!
Let us improve this post!
Tell us how we can improve this post?

Patty Mulder
Patty Mulder is an Dutch expert on Management Skills, Personal Effectiveness and Business Communication. She is also a Content writer, Business Coach and Company Trainer and lives in the Netherlands (Europe). Note: all her articles are written in Dutch and we translated her articles to English!
Related ARTICLES


DevOps methodology explained

RASCI Chart explained including an example

Learning Management System (LMS)

Stage Gate Process by Robert Cooper explained

Test Driven Development (TDD)

Feature Driven Development Methodology (FDD)
Also interesting.

Gantt Chart explained plus template

Prince2 Methodology: Phases and Principles

Responsibility Assignment Matrix: the Basics and Template
One response to “moscow method of prioritization explained”.
Thanks for providing a concise and easily understandable explanation. The one thing that stood out to me however, is the example for the Should Have section. Tow bars are clearly “Could have” at best and in this situation would probably end up in the “Won’t have” bucket simply because there’s no justification for them at all on an experimental vehicle that will not be driven on a public road. To make this more believable I’d recommend changing the example for “Should Haves” to either: Seats – the vehicle should have a seat for the driver but as long as someone can drive it somehow it’s not critical. Or Steering Wheel – ideally the vehicle should have a steering wheel, but as long as it CAN be steered (perhaps by levers) then the project will pass. Otherwise, this is a really useful article. Thanks again.
Leave a Reply Cancel reply
You must be logged in to post a comment.
BOOST YOUR SKILLS
Toolshero supports people worldwide ( 10+ million visitors from 100+ countries ) to empower themselves through an easily accessible and high-quality learning platform for personal and professional development.
By making access to scientific knowledge simple and affordable, self-development becomes attainable for everyone, including you! Join our learning platform and boost your skills with Toolshero.

POPULAR TOPICS
- Change Management
- Marketing Theories
- Problem Solving Theories
- Psychology Theories
ABOUT TOOLSHERO
- Free Toolshero e-book
- Memberships & Pricing
- TPC and eLearning
- What's NEW at TPC?
- Read Watch Interact
- Practice Review Test
- Teacher-Tools
- Request a Demo
- Get A Quote
- Subscription Selection
- Seat Calculator
- Ad Free Account
- Edit Profile Settings
- Metric Conversions Questions
- Metric System Questions
- Metric Estimation Questions
- Significant Digits Questions
- Proportional Reasoning
- Acceleration
- Distance-Displacement
- Dots and Graphs
- Graph That Motion
- Match That Graph
- Name That Motion
- Motion Diagrams
- Pos'n Time Graphs Numerical
- Pos'n Time Graphs Conceptual
- Up And Down - Questions
- Balanced vs. Unbalanced Forces
- Change of State
- Force and Motion
- Mass and Weight
- Match That Free-Body Diagram
- Net Force (and Acceleration) Ranking Tasks
- Newton's Second Law
- Normal Force Card Sort
- Recognizing Forces
- Air Resistance and Skydiving
- Solve It! with Newton's Second Law
- Which One Doesn't Belong?
- Component Addition Questions
- Head-to-Tail Vector Addition
- Projectile Mathematics
- Trajectory - Angle Launched Projectiles
- Trajectory - Horizontally Launched Projectiles
- Vector Addition
- Vector Direction
- Which One Doesn't Belong? Projectile Motion
- Forces in 2-Dimensions
- Being Impulsive About Momentum
- Explosions - Law Breakers
- Hit and Stick Collisions - Law Breakers
- Case Studies: Impulse and Force
- Impulse-Momentum Change Table
- Keeping Track of Momentum - Hit and Stick
- Keeping Track of Momentum - Hit and Bounce
- What's Up (and Down) with KE and PE?
- Energy Conservation Questions
- Energy Dissipation Questions
- Energy Ranking Tasks
- LOL Charts (a.k.a., Energy Bar Charts)
- Match That Bar Chart
- Words and Charts Questions
- Name That Energy
- Stepping Up with PE and KE Questions
- Case Studies - Circular Motion
- Circular Logic
- Forces and Free-Body Diagrams in Circular Motion
- Gravitational Field Strength
- Universal Gravitation
- Angular Position and Displacement
- Linear and Angular Velocity
- Angular Acceleration
- Rotational Inertia
- Balanced vs. Unbalanced Torques
- Getting a Handle on Torque
- Torque-ing About Rotation
- Properties of Matter
- Fluid Pressure
- Buoyant Force
- Sinking, Floating, and Hanging
- Pascal's Principle
- Flow Velocity
- Bernoulli's Principle
- Balloon Interactions
- Charge and Charging
- Charge Interactions
- Charging by Induction
- Conductors and Insulators
- Coulombs Law
- Electric Field
- Electric Field Intensity
- Polarization
- Case Studies: Electric Power
- Know Your Potential
- Light Bulb Anatomy
- I = ∆V/R Equations as a Guide to Thinking
- Parallel Circuits - ∆V = I•R Calculations
- Resistance Ranking Tasks
- Series Circuits - ∆V = I•R Calculations
- Series vs. Parallel Circuits
- Equivalent Resistance
- Period and Frequency of a Pendulum
- Pendulum Motion: Velocity and Force
- Energy of a Pendulum
- Period and Frequency of a Mass on a Spring
- Horizontal Springs: Velocity and Force
- Vertical Springs: Velocity and Force
- Energy of a Mass on a Spring
- Decibel Scale
- Frequency and Period
- Closed-End Air Columns
- Name That Harmonic: Strings
- Rocking the Boat
- Wave Basics
- Matching Pairs: Wave Characteristics
- Wave Interference
- Waves - Case Studies
- Color Addition and Subtraction
- Color Filters
- If This, Then That: Color Subtraction
- Light Intensity
- Color Pigments
- Converging Lenses
- Curved Mirror Images
- Law of Reflection
- Refraction and Lenses
- Total Internal Reflection
- Who Can See Who?
- Formulas and Atom Counting
- Lab Equipment
- Atomic Models
- Bond Polarity
- Entropy Questions
- Cell Voltage Questions
- Heat of Formation Questions
- Reduction Potential Questions
- Oxidation States Questions
- Measuring the Quantity of Heat
- Hess's Law
- Oxidation-Reduction Questions
- Galvanic Cells Questions
- Thermal Stoichiometry
- Molecular Polarity
- Quantum Mechanics
- Balancing Chemical Equations
- Bronsted-Lowry Model of Acids and Bases
- Classification of Matter
- Collision Model of Reaction Rates
- Density Ranking Tasks
- Dissociation Reactions
- Complete Electron Configurations
- Elemental Measures
- Enthalpy Change Questions
- Equilibrium Concept
- Equilibrium Constant Expression
- Equilibrium Calculations - Questions
- Equilibrium ICE Table
- Intermolecular Forces Questions
- Ionic Bonding
- Lewis Electron Dot Structures
- Limiting Reactants
- Line Spectra Questions
- Mass Stoichiometry
- Measurement and Numbers
- Metals, Nonmetals, and Metalloids
- Metric Estimations
- Metric System
- Molarity Ranking Tasks
- Mole Conversions
- Name That Element
- Names to Formulas
- Names to Formulas 2
- Nuclear Decay
- Particles, Words, and Formulas
- Periodic Trends
- Precipitation Reactions and Net Ionic Equations
- Pressure Concepts
- Pressure-Temperature Gas Law
- Pressure-Volume Gas Law
- Chemical Reaction Types
- Significant Digits and Measurement
- States Of Matter Exercise
- Stoichiometry Law Breakers
- Stoichiometry - Math Relationships
- Subatomic Particles
- Spontaneity and Driving Forces
- Gibbs Free Energy
- Volume-Temperature Gas Law
- Acid-Base Properties
- Energy and Chemical Reactions
- Chemical and Physical Properties
- Valence Shell Electron Pair Repulsion Theory
- Writing Balanced Chemical Equations
- Mission CG1
- Mission CG10
- Mission CG2
- Mission CG3
- Mission CG4
- Mission CG5
- Mission CG6
- Mission CG7
- Mission CG8
- Mission CG9
- Mission EC1
- Mission EC10
- Mission EC11
- Mission EC12
- Mission EC2
- Mission EC3
- Mission EC4
- Mission EC5
- Mission EC6
- Mission EC7
- Mission EC8
- Mission EC9
- Mission RL1
- Mission RL2
- Mission RL3
- Mission RL4
- Mission RL5
- Mission RL6
- Mission KG7
- Mission RL8
- Mission KG9
- Mission RL10
- Mission RL11
- Mission RM1
- Mission RM2
- Mission RM3
- Mission RM4
- Mission RM5
- Mission RM6
- Mission RM8
- Mission RM10
- Mission LC1
- Mission RM11
- Mission LC2
- Mission LC3
- Mission LC4
- Mission LC5
- Mission LC6
- Mission LC8
- Mission SM1
- Mission SM2
- Mission SM3
- Mission SM4
- Mission SM5
- Mission SM6
- Mission SM8
- Mission SM10
- Mission KG10
- Mission SM11
- Mission KG2
- Mission KG3
- Mission KG4
- Mission KG5
- Mission KG6
- Mission KG8
- Mission KG11
- Mission F2D1
- Mission F2D2
- Mission F2D3
- Mission F2D4
- Mission F2D5
- Mission F2D6
- Mission KC1
- Mission KC2
- Mission KC3
- Mission KC4
- Mission KC5
- Mission KC6
- Mission KC7
- Mission KC8
- Mission AAA
- Mission SM9
- Mission LC7
- Mission LC9
- Mission NL1
- Mission NL2
- Mission NL3
- Mission NL4
- Mission NL5
- Mission NL6
- Mission NL7
- Mission NL8
- Mission NL9
- Mission NL10
- Mission NL11
- Mission NL12
- Mission MC1
- Mission MC10
- Mission MC2
- Mission MC3
- Mission MC4
- Mission MC5
- Mission MC6
- Mission MC7
- Mission MC8
- Mission MC9
- Mission RM7
- Mission RM9
- Mission RL7
- Mission RL9
- Mission SM7
- Mission SE1
- Mission SE10
- Mission SE11
- Mission SE12
- Mission SE2
- Mission SE3
- Mission SE4
- Mission SE5
- Mission SE6
- Mission SE7
- Mission SE8
- Mission SE9
- Mission VP1
- Mission VP10
- Mission VP2
- Mission VP3
- Mission VP4
- Mission VP5
- Mission VP6
- Mission VP7
- Mission VP8
- Mission VP9
- Mission WM1
- Mission WM2
- Mission WM3
- Mission WM4
- Mission WM5
- Mission WM6
- Mission WM7
- Mission WM8
- Mission WE1
- Mission WE10
- Mission WE2
- Mission WE3
- Mission WE4
- Mission WE5
- Mission WE6
- Mission WE7
- Mission WE8
- Mission WE9
- Vector Walk Interactive
- Name That Motion Interactive
- Kinematic Graphing 1 Concept Checker
- Kinematic Graphing 2 Concept Checker
- Graph That Motion Interactive
- Two Stage Rocket Interactive
- Rocket Sled Concept Checker
- Force Concept Checker
- Free-Body Diagrams Concept Checker
- Free-Body Diagrams The Sequel Concept Checker
- Skydiving Concept Checker
- Elevator Ride Concept Checker
- Vector Addition Concept Checker
- Vector Walk in Two Dimensions Interactive
- Name That Vector Interactive
- River Boat Simulator Concept Checker
- Projectile Simulator 2 Concept Checker
- Projectile Simulator 3 Concept Checker
- Hit the Target Interactive
- Turd the Target 1 Interactive
- Turd the Target 2 Interactive
- Balance It Interactive
- Go For The Gold Interactive
- Egg Drop Concept Checker
- Fish Catch Concept Checker
- Exploding Carts Concept Checker
- Collision Carts - Inelastic Collisions Concept Checker
- Its All Uphill Concept Checker
- Stopping Distance Concept Checker
- Chart That Motion Interactive
- Roller Coaster Model Concept Checker
- Uniform Circular Motion Concept Checker
- Horizontal Circle Simulation Concept Checker
- Vertical Circle Simulation Concept Checker
- Race Track Concept Checker
- Gravitational Fields Concept Checker
- Orbital Motion Concept Checker
- Angular Acceleration Concept Checker
- Balance Beam Concept Checker
- Torque Balancer Concept Checker
- Aluminum Can Polarization Concept Checker
- Charging Concept Checker
- Name That Charge Simulation
- Coulomb's Law Concept Checker
- Electric Field Lines Concept Checker
- Put the Charge in the Goal Concept Checker
- Circuit Builder Concept Checker (Series Circuits)
- Circuit Builder Concept Checker (Parallel Circuits)
- Circuit Builder Concept Checker (∆V-I-R)
- Circuit Builder Concept Checker (Voltage Drop)
- Equivalent Resistance Interactive
- Pendulum Motion Simulation Concept Checker
- Mass on a Spring Simulation Concept Checker
- Particle Wave Simulation Concept Checker
- Boundary Behavior Simulation Concept Checker
- Slinky Wave Simulator Concept Checker
- Simple Wave Simulator Concept Checker
- Wave Addition Simulation Concept Checker
- Standing Wave Maker Simulation Concept Checker
- Color Addition Concept Checker
- Painting With CMY Concept Checker
- Stage Lighting Concept Checker
- Filtering Away Concept Checker
- InterferencePatterns Concept Checker
- Young's Experiment Interactive
- Plane Mirror Images Interactive
- Who Can See Who Concept Checker
- Optics Bench (Mirrors) Concept Checker
- Name That Image (Mirrors) Interactive
- Refraction Concept Checker
- Total Internal Reflection Concept Checker
- Optics Bench (Lenses) Concept Checker
- Kinematics Preview
- Velocity Time Graphs Preview
- Moving Cart on an Inclined Plane Preview
- Stopping Distance Preview
- Cart, Bricks, and Bands Preview
- Fan Cart Study Preview
- Friction Preview
- Coffee Filter Lab Preview
- Friction, Speed, and Stopping Distance Preview
- Up and Down Preview
- Projectile Range Preview
- Ballistics Preview
- Juggling Preview
- Marshmallow Launcher Preview
- Air Bag Safety Preview
- Colliding Carts Preview
- Collisions Preview
- Engineering Safer Helmets Preview
- Push the Plow Preview
- Its All Uphill Preview
- Energy on an Incline Preview
- Modeling Roller Coasters Preview
- Hot Wheels Stopping Distance Preview
- Ball Bat Collision Preview
- Energy in Fields Preview
- Weightlessness Training Preview
- Roller Coaster Loops Preview
- Universal Gravitation Preview
- Keplers Laws Preview
- Kepler's Third Law Preview
- Charge Interactions Preview
- Sticky Tape Experiments Preview
- Wire Gauge Preview
- Voltage, Current, and Resistance Preview
- Light Bulb Resistance Preview
- Series and Parallel Circuits Preview
- Thermal Equilibrium Preview
- Linear Expansion Preview
- Heating Curves Preview
- Electricity and Magnetism - Part 1 Preview
- Electricity and Magnetism - Part 2 Preview
- Vibrating Mass on a Spring Preview
- Period of a Pendulum Preview
- Wave Speed Preview
- Slinky-Experiments Preview
- Standing Waves in a Rope Preview
- Sound as a Pressure Wave Preview
- DeciBel Scale Preview
- DeciBels, Phons, and Sones Preview
- Sound of Music Preview
- Shedding Light on Light Bulbs Preview
- Models of Light Preview
- Electromagnetic Radiation Preview
- Electromagnetic Spectrum Preview
- EM Wave Communication Preview
- Digitized Data Preview
- Light Intensity Preview
- Concave Mirrors Preview
- Object Image Relations Preview
- Snells Law Preview
- Reflection vs. Transmission Preview
- Magnification Lab Preview
- Reactivity Preview
- Ions and the Periodic Table Preview
- Periodic Trends Preview
- Chemical Reactions Preview
- Intermolecular Forces Preview
- Melting Points and Boiling Points Preview
- Bond Energy and Reactions Preview
- Reaction Rates Preview
- Ammonia Factory Preview
- Stoichiometry Preview
- Nuclear Chemistry Preview
- Gaining Teacher Access
- Task Tracker Directions
- Conceptual Physics Course
- On-Level Physics Course
- Honors Physics Course
- Chemistry Concept Builders
- All Chemistry Resources
- Users Voice
- Tasks and Classes
- Webinars and Trainings
- Subscription
- Subscription Locator
- 1-D Kinematics
- Newton's Laws
- Vectors - Motion and Forces in Two Dimensions
- Momentum and Its Conservation
- Work and Energy
- Circular Motion and Satellite Motion
- Thermal Physics
- Static Electricity
- Electric Circuits
- Vibrations and Waves
- Sound Waves and Music
- Light and Color
- Reflection and Mirrors
- About the Physics Interactives
- Task Tracker
- Usage Policy
- Newtons Laws
- Vectors and Projectiles
- Forces in 2D
- Momentum and Collisions
- Circular and Satellite Motion
- Balance and Rotation
- Electromagnetism
- Waves and Sound
- Atomic Physics
- Forces in Two Dimensions
- Work, Energy, and Power
- Circular Motion and Gravitation
- Sound Waves
- 1-Dimensional Kinematics
- Circular, Satellite, and Rotational Motion
- Einstein's Theory of Special Relativity
- Waves, Sound and Light
- QuickTime Movies
- About the Concept Builders
- Pricing For Schools
- Directions for Version 2
- Measurement and Units
- Relationships and Graphs
- Rotation and Balance
- Vibrational Motion
- Reflection and Refraction
- Teacher Accounts
- Kinematic Concepts
- Kinematic Graphing
- Wave Motion
- Sound and Music
- About CalcPad
- 1D Kinematics
- Vectors and Forces in 2D
- Simple Harmonic Motion
- Rotational Kinematics
- Rotation and Torque
- Rotational Dynamics
- Electric Fields, Potential, and Capacitance
- Transient RC Circuits
- Light Waves
- Units and Measurement
- Stoichiometry
- Molarity and Solutions
- Thermal Chemistry
- Acids and Bases
- Kinetics and Equilibrium
- Solution Equilibria
- Oxidation-Reduction
- Nuclear Chemistry
- Newton's Laws of Motion
- Work and Energy Packet
- Static Electricity Review
- NGSS Alignments
- 1D-Kinematics
- Projectiles
- Circular Motion
- Magnetism and Electromagnetism
- Graphing Practice
- About the ACT
- ACT Preparation
- For Teachers
- Other Resources
- Solutions Guide
- Solutions Guide Digital Download
- Motion in One Dimension
- Work, Energy and Power
- Chemistry of Matter
- Measurement and the Metric System
- Algebra Based On-Level Physics
- Honors Physics
- Conceptual Physics
- Other Tools
- Frequently Asked Questions
- Purchasing the Download
- Purchasing the Digital Download
- About the NGSS Corner
- NGSS Search
- Force and Motion DCIs - High School
- Energy DCIs - High School
- Wave Applications DCIs - High School
- Force and Motion PEs - High School
- Energy PEs - High School
- Wave Applications PEs - High School
- Crosscutting Concepts
- The Practices
- Physics Topics
- NGSS Corner: Activity List
- NGSS Corner: Infographics
- About the Toolkits
- Position-Velocity-Acceleration
- Position-Time Graphs
- Velocity-Time Graphs
- Newton's First Law
- Newton's Second Law
- Newton's Third Law
- Terminal Velocity
- Projectile Motion
- Forces in 2 Dimensions
- Impulse and Momentum Change
- Momentum Conservation
- Work-Energy Fundamentals
- Work-Energy Relationship
- Roller Coaster Physics
- Satellite Motion
- Electric Fields
- Circuit Concepts
- Series Circuits
- Parallel Circuits
- Describing-Waves
- Wave Behavior Toolkit
- Standing Wave Patterns
- Resonating Air Columns
- Wave Model of Light
- Plane Mirrors
- Curved Mirrors
- Teacher Guide
- Using Lab Notebooks
- Current Electricity
- Light Waves and Color
- Reflection and Ray Model of Light
- Refraction and Ray Model of Light
- Teacher Resources
- Subscriptions

- Newton's Laws
- Einstein's Theory of Special Relativity
- About Concept Checkers
- School Pricing
- Newton's Laws of Motion
- Newton's First Law
- Newton's Third Law
Mechanics: Work, Energy and Power
Work, energy and power: problem set overview.
There are 20 ready-to-use problem sets on the topic of Work, Energy, and Power. The problems target your ability to use equations related to work and power, to calculate the kinetic, potential and total mechanical energy, and to use the work-energy relationship in order to determine the final speed, stopping distance or final height of an object.
Work results when a force acts upon an object to cause a displacement (or a motion) or, in some instances, to hinder a motion of a moving object. Three variables are of importance in this definition - force, displacement, and the extent to which the force causes or hinders the displacement. Each of these three variables find their way into the equation for work. That equation is:
Work = Force • Displacement • Cosine(theta)
W = F • d • cos(Θ)
Since the standard metric unit of force is the Newton and the standard meteric unit of displacement is the meter, then the standard metric unit of work is a Newton•meter, defined as a Joule and abbreviated with a J.
The most complicated part of the work equation and work calculations is the meaning of the angle theta (Θ) in the above equation. The angle is not just any stated angle in the problem; it is the angle between the F and the d vectors. In solving work problems, one must always be aware of this definition - theta is the angle between the force and the displacement which it causes. If the force is in the same direction as the displacement, then the angle is 0 degrees. If the force is in the opposite direction as the displacement, then the angle is 180 degrees. If the force is up and the displacement is to the right, then the angle is 90 degrees. This is summarized in the graphic below.
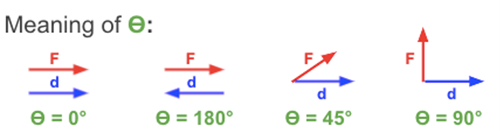
Power is defined as the rate at which work is done upon an object. Like all rate quantities, power is a time-based quantity. Power is related to how fast a job is done. Two identical jobs or tasks can be done at different rates - one slowly or and one rapidly. The work is the same in each case (since they are identical jobs) but the power is different. The equation for power shows the importance of time:
Power = Work / time
The unit for standard metric work is the Joule and the standard metric unit for time is the second, so the standard metric unit for power is a Joule / second, defined as a Watt and abbreviated W . Special attention should be taken so as not to confuse the unit Watt, abbreviated W, with the quantity work, also abbreviated by the letter W.
Combining the equations for power and work can lead to a second equation for power. Power is W/t and work is F•d•cos(theta). Substituting the expression for work into the power equation yields P = F•d•cos(theta)/t. If this equation is re-written as
P = F • cos(Θ) • (d/t)
one notices a simplification which could be made. The d/t ratio is the speed value for a constant speed motion or the average speed for an accelerated motion. Thus, the equation can be re-written as
P = F • v • cos(Θ)
where v is the constant speed or the average speed value. A few of the problems in these problem sets will utilize this derived equation for power.
Mechanical, Kinetic and Potential Energies
There are two forms of mechanical energy - potential energy and kinetic energy.
Potential energy is the stored energy of position. In this set of problems, we will be most concerned with the stored energy due to the vertical position of an object within Earth's gravitational field. Such energy is known as the gravitational potential energy ( PE grav ) and is calculated using the equation
PE grav = m•g•h
where m is the mass of the object (with standard units of kilograms), g is the gravitational field constant (9.8 N/kg) and h is the height of the object (with standard units of meters) above some arbitraily defined zero level (such as the ground or the top of a lab table in a physics room). Potential energy can also be stored in a mass-spring system. This is known as elastic potential energy ( PE elastic ). As a spring is stretched some distance x from its equilibrium position, potential energy is stored in the spring-mass system. This type of potential energy is calculated using the equation
PE elastic = 1/2• k • x 2
where x is the amount of stretch from the equilibrium position and k is the spring constant of the spring.
Kinetic energy is defined as the energy possessed by an object due to its motion. An object must be moving to possess kinetic energy. The amount of kinetic energy ( KE ) possessed by a moving object is dependent upon mass and speed. The equation for kinetic energy is
KE = 0.5 • m • v 2
where m is the mass of the object (with standard units of kilograms) and v is the speed of the object (with standard units of m/s).
The total mechanical energy possessed by an object is the sum of its kinetic and potential energies.
Work-Energy Connection
There is a relationship between work and total mechanical energy. The relationship is best expressed by the equation
TME i + W nc = TME f
In words, this equation says that the initial amount of total mechanical energy ( TME i ) of a system is altered by the work which is done to it by non-conservative forces ( W nc ). The final amount of total mechanical energy ( TME f ) possessed by the system is equivalent to the initial amount of energy ( TME i ) plus the total work done by these non-conservative forces ( W nc ).
The mechanical energy possessed by a system is the sum of the kinetic energy and the potential energy. Thus the above equation can be re-arranged to the form of
KE i + PE i + W nc = KE f + PE f
0.5 • m • v i 2 + m • g • h i + F • d • cos(Θ) = 0.5 • m • v f 2 + m • g • h f
The work done to a system by non-conservative forces (W nc ) can be described as either positive work or negative work. Positive work is done on a system when the force doing the work acts in the direction of the motion of the object. Negative work is done when the force doing the work opposes the motion of the object. When a positive value for work is substituted into the work-energy equation above, the final amount of energy will be greater than the initial amount of energy; the system is said to have gained mechanical energy. When a negative value for work is substituted into the work-energy equation above, the final amount of energy will be less than the initial amount of energy; the system is said to have lost mechanical energy. There are occasions in which the only forces doing work are conservative forces (sometimes referred to as internal forces). Typically, such conservative forces include gravitational forces, elastic or spring forces, electrical forces and magnetic forces. When the only forces doing work are conservative forces, then the W nc term in the equation above is zero. In such instances, the system is said to have conserved its mechanical energy.
The proper approach to a work-energy problem involves carefully reading the problem description and substituting values from it into the work-energy equation listed above. Inferences about certain terms will have to be made based on a conceptual understanding of kinetic and potential energy. For instance, if the object is initially on the ground, then it can be inferred that the PE i is 0 and that term can be canceled from the work-energy equation. In other instances, the height of the object is the same in the initial state as in the final state, so the PE i and the PE f terms are the same. As such, they can be mathematically canceled from each side of the equation. In other instances, the speed is constant during the motion, so the KE i and KE f terms are the same and can thus be mathematically canceled from each side of the equation. Finally, there are instances in which the KE and or the PE terms are not stated; rather, the mass (m), speed (v), and height (h) is given. In such instances, the KE and PE terms can be determined using their respective equations. Make it your habit from the beginning to simply start with the work and energy equation, to cancel terms which are zero or unchanging, to substitute values of energy and work into the equation and to solve for the stated unknown.
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., m = 1.50 kg, v i = 2.68 m/s, F = 4.98 N, t = 0.133 s, v f = ???).
- ...plots a strategy for solving for the unknown quantity. The strategy will typically center saround the use of physics equations and is heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...
Additional Readings/Study Aids:
The following pages from The Physics Classroom tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.
- Sample Work Calculations
- Resolving the Weight Vector on an Inclined Plane
- Potential Energy
- Kinetic Energy
- Mechanical Energy
- Situations Involving External Forces
- Situations Involving Energy Conservation
Watch a Video
We have developed and continue to develop Video Tutorials on introductory physics topics. You can find these videos on our YouTube channel . We have an entire Playlist on the topic of Work and Energy .


- Your Project
- MoSCoW Method
What is the MoSCoW Method?
The MoSCoW Method is a prioritization tool that helps professionals in managing their time and effort .
To do so, it proposes to classify the importance of the different characteristics of a product (or a Project) according to their importance .
Its name is an acronym of the 4 Prioritization Categories proposed (adding two “o”):
- M ust Have .
- S hould Have .
- C ould Have .
- W on’t Have .
Four Prioritization Categories
Must Have : Essential Requirements that the product or project must have.
- Critical Features without replacement.
Should Have : Important desired Requirements for the product or project.
- They can be substituted if necessary.
Could Have : Improvements to the product or project.
- There are different alternatives.
Won’t have : Characteristics agreed not to be adopted .
- No one will waste time implementing them.
Let’s see the first example:
MoSCoW Method example

Imagine that you have been hired to create a Website for a Law firm.
They want a professional Site where people can Register and, once inside, track their court cases .
Since you want to deliver the best possible Site on time, you decide to follow the MoSCoW method .
How does it look like?
Must Have :
- Solid programming without any bugs.
- A Solid Register System.
- A Safe and Reliable personal directory.
Should Have :
- A Fast Site.
- An outstanding Design.
- Notifications sent by e-mail.
Could Have :
- Custom menus.
- Suggestions.
- A Blog section with latest news.
Won’t Have :
- Paid content.
- A Public Members section.
As we usually say, this Method may seem obvious.
Then… Why is it important?
Why is the MoSCoW Method important?
Many of professionals end up wasting time , effort and resources on useless task s that are ultimately not essential at all.
Surely you have experienced this situation working in a Team:
- Everyone spends hours modifying a minor feature and, ultimately, the important thing is missing .
That is why this Method is so important:
- Because it concentrates your efforts and forces you to think about what is really important .
As you can imagine, this Tool can be employed in practically all kinds of situations.
But when do we especially recommend it?
When should you use the MoSCoW Method?
We highly recommend to use the MoSCoW Method:
- To put order and prioritization.
- To avoid wasting time with non-essential touch-ups.
- In order to meet the Essential Requirements.
- When the product can have very different characteristics.
Now, let’s see more examples:
MoSCoW Method examples
We have chosen different real examples where the MoSCoW Method can be of great help for the development of certain products.
Let’s begin:
A Wallet - MoSCoW Method example

Let’s imagine that you are developing a wallet .
As you know, wallets are very modular products.
They can have:
- Several or few departments for cards.
- Coin purse… or not.
- 1 or 2 bill slots.
There is not a canonical wallet (one that is the benchmark for all the others).
- That is why you decided to use the MoSCoW Method to develop it.
After some thoughts, you decide that your wallet:
- 2 bill slots.
- 8 compartments for credit cards.
- High resistance materials and sewing.
- Leather as its main material.
- A translucid Credit card compartment.
- A transverse horizontal compartment.
- A striking color on the inside of the bill slots.
- Completely black exterior color.
- One translucid compartment for small photos.
- A Coin purse.
- A Passport compartment.
Making a Cake - MoSCoW Method example

In this example, we’ll imagine that you are preparing a wedding Cake .
- You have a very rigid deadline (the wedding day, of course).
In addition, as you also know, Cakes can have lots of variations.
- We could say they are very modular .
That is why you decide to use the MoSCoW Method.
How does it look?
Well, your Cake:
- White coating.
- Two sugar figurines on top.
- 6 layers of sponge cake inside.
- Belgian chocolate between the layers.
- Decorations on the edges
- Sugar flowers.
- Chocolate balls.
- Scattered sugar pearls.
- Multicolor layers.
- An excessive amount of decoration.
- Fruit flavor.
Designing a Poster - MoSCoW Method example

You are now an artist hired to Design a poster for a Rock concert.
Obviously, this is a Design job with infinite variations possible.
- Also, you have a close deadline to finish it.
No need to mention that you will use the MoSCoW Method.
Finally, the Poster:
- The name of the Main rock band, very prominent.
- Images and colors that best suit their style.
- A typeface that best suits the musical style.
- An illustration related to Rock in the middle.
- The name of the rest of the bands that will play.
- Where and when it will take place.
- Where you can buy the tickets.
- Nearby metro and bus stations.
- The name of the city.
- The maximum capacity of the stadium
- At what time each band will play.
Summarizing
The MoSCoW Method is a prioritization tool that helps professionals in managing their time and effort.
It proposes to classify the importance of the different characteristics of a product in 4 Categories :
- M ust Have.
- S hould Have.
- C ould Have.
- W on’t Have.
Although this Method can be used in all kinds of situations, we highly recommend to use it:
- When working in a team .
- In Design tasks .
- When there is a close deadline .
- With modular products or projects .
- Economies of Scale
- Business Plan for Beginners
- Business Plan Basics
- How to write a Business Plan
- Cash Flow Calculation
- Raising Funds for a Business
- 4 C’s of Credit
- Business Plan Templates
- Customer Insight
- Customer Experience
- Customer Pain Points
- 4C Marketing Model
- RATER Model
- Augmented Product
- Product Mix
- Unique Selling Proposition
- DAGMAR Model
- Marketing Storytelling
- Content Marketing
- Psychographics
- Barnum Effect
- Market Segmentation
- Market Research & Big Data
- Marketing to Generation Z
- 4P Marketing Mix
- 7P Marketing Mix
- Sales Funnel
- Loyalty Ladder
- RACE Planning
- Push and Pull Marketing
- Marketing Strategy
- Marketing Templates
- Starting your own business
- From Startup to a Business
- Entrepreneur FAQs
- Start your Business Idea
- Entrepreneur Golden Rules
- Innovate or Imitate?
- Design Thinking
- SCAMPER Model
- AAR Process
- Work From Home
- Growth strategies for Startups
- VMOST Analysis
- 3P Framework
- SOAR Analysis
- TELOS Analysis
- 5 C’s of Entrepreneurship
- Crowdfunding
- BATNA & ZOPA Negotiation
- Entrepreneur with no Money
- Entrepreneurship Templates
- Strategy vs Tactics
- Mission and Vision
- Business Values
- Value Chain
- Scenario Planning
- Porter 6 Forces
- Bowman’s Strategy Clock
- GE-McKinsey Matrix
- Delta Model
- PEST Analysis
- PESTEL Analysis
- SWOT Analysis
- VRIO Framework
- Strategy Canvas
- Competitive Advantages
- Porter’s Four Corners
- 5 Ps of Strategy
- Porter’s Generic Strategies
- Porter’s Diamond Model
- Wardley Map
- Core Competencies
- Resource Based View
- Bridges Transition Model
- CAGE Distance Framework
- McKinsey’s 3 Horizons
- Vertical Integration
- Horizontal Integration
- Blue Ocean Strategy
- Red Ocean Strategy
- Porter 5 Forces
- Ansoff Matrix
- McKinsey 7S Framework
- CATWOE Analysis
- Strategy Pyramid
- Bain’s RAPID Framework
- Balanced Scorecard
- Resources and Capabilities
- Strategy of Apple
- Strategy of Amazon
- Strategy of Starbucks
- Strategy Templates
- Communicate Effectively
- COIN Conversation Model
- SCARF Model
- SBI Feedback Model
- CEDAR Feedback Model
- How to behave at a meeting
- Gibbs’ Reflective Cycle
- Bloom’s Taxonomy
- 5E Learning Model
- 9-Box Performance Grid
- SEEDS Bias Model
- Halo Effect
- Pygmalion Rosenthal Effect
- Dunning-Kruger Effect
- How to be an Entrepreneur
- How to be a Leader
- Mintzberg Managerial Roles
- Cog’s Ladder
- The Peter Principle
- How to Negotiate
- Teamwork Skills and Profiles
- Gantt Chart
- RACI Matrix
- Eisenhower Matrix
- FMEA Process
- Problem Solving
- Ishikawa Fishbone diagram
- 5 Whys Method
- 8 Disciplines Method
- ADDIE Model
- ORAPAPA Method
- Cynefin Framework
- Just In Time
- SMART Goals
- KISS Principle
- Birkinshaw’s 4 Dimensions
- Parkinson’s Law
- OGSM Framework
- OKR Methodology
- APQP Framework
- Theory of Constraints
- Success through Organization
- ADKAR Model
- Lewin’s Change Model
- Kotter’s 8-Step Model
- The Greiner Curve
- GAP Analysis
- Planning Templates
- Mean, Median and Mode
- Define your Data
- Pareto Principle 80/20 Rule
- Decision Matrix
- Decision Tree
- TARA Framework
- Root Cause Analysis
- Simplex Process
- Forecasting Methods
- Product Life Cycle
- How to use Google Trends
- Correlation vs Causation
© 2024 - Consuunt .
We're not around right now. But you can send us an email and we'll get back to you, asap.
Log in with your credentials
Forgot your details.

Guide: MoSCoW Method
Author: Daniel Croft
Daniel Croft is an experienced continuous improvement manager with a Lean Six Sigma Black Belt and a Bachelor's degree in Business Management. With more than ten years of experience applying his skills across various industries, Daniel specializes in optimizing processes and improving efficiency. His approach combines practical experience with a deep understanding of business fundamentals to drive meaningful change.
The MoSCoW Method transcends being just a prioritization tool; it is a strategic approach for navigating the intricate decision-making in project management. This methodology excels by offering a structured framework, facilitating discussions among stakeholders to assess and align on the relative importance of various tasks and features in a project.
Central to MoSCoW is its acronym, denoting four priority categories – Must have, Should have, Could have, and Won’t have. This classification is crucial in managing stakeholder expectations, directing the project team’s focus towards critical elements, and charting a clear course for project advancement.
What is the MoSCoW Method?
The MoSCoW method is used as a prioritization tool, but it is more than just that; it is also a strategic approach to handling complex decision-making processes that you can encounter in project management. This method shines by offering a structured framework for stakeholders to discuss, debate, and ultimately agree on the relative importance of different tasks or features within a project.
The uniqueness of the MoSCoW method is within its acronym, which represents four priority categories. Must have, Should have, Could have, and Won’t have. This structure is key to managing stakeholder expectations and ensuring that a project team focuses on the most crucial elements first, setting a clear path for project progression.
The MoSCoW Categories

In the ‘ Must have ‘ category, you find the key activities that are essential to your project . These are non-negotiable and pivotal for the project’s success. This category often comprises items that, if omitted, would make the project irrelevant or non-compliant with essential criteria like legal standards or core objectives.
Should Have
Moving to the ‘ Should have ‘ category, we encounter important elements that, while not critical to the project’s existence, greatly enhance its value and effectiveness . These are features that stakeholders strongly desire, and their inclusion could significantly enhance the project’s outcome . However, their absence wouldn’t label the project a failure.
The ‘ Could have ‘ category is where you place desirable but less critical elements . These are often enhancements that would be nice to include but aren’t vital to the project’s success . The inclusion of these elements is usually subject to resource availability and project timelines.
The ‘ Won’t have ‘ category is often misunderstood but is crucial for setting realistic boundaries. It includes elements that, although potentially beneficial, are beyond the scope of the current project phase or constraints. This clear demarcation helps manage expectations and focus on what’s achievable within the project’s constraints.
How to Apply the MoSCoW Method: A Step-by-Step Guide
Implementing the MoSCoW Method in a project requires a systematic approach, ensuring that all aspects of the project are considered and aligned with the prioritization framework. Here’s a detailed look into each step of implementing this method:
Step 1: Gather Requirements
The first step in the MoSCoW method requires gathering a list of the tasks , activities, features, or requirements you need to prioritize in your project. For this step, you should engage with all relevant stakeholders , including project sponsors, end-users, and technical teams. This ensures that the requirements reflect a wide range of perspectives and needs.
To help decide the categorize of each task in a later step you should understand the overall goals of the project . You will also need to gain an understanding of technical, business, time, and resource constraints right from the start. This helps in setting realistic expectations for what can be achieved.
Step 2: Categories Each Requirement
The next step is to, as a team with the relevant stakeholders, run a categorization session . Doing this with the stakeholders involved will help to gain buy-in and support for the project as well as a shared understanding of priorities.
Each requirement’s placement in the MoSCoW categories should be a subject of discussion. Different stakeholders may have varying views on what is a ‘ Must have ‘ or ‘ Should have ‘, and these need to be reconciled.
For each decision, documenting the rationale behind the categorization can be valuable, especially for future reference or when explaining decisions to others not involved in the process.
Step 3: Review and Adjust
You will need to ensure the decisions of the categories are balanced and achievable within the scope once all are allocated. You may find that you still have too many must-haves and should-haves that either some activities need to be downgraded or a consideration to go back to decision-makers and create a case for more resources of time to achieve what is needed.
Step 4: Use as a Guiding Tool
You should continue to use the MoSCoW prioritization to inform decisions throughout the project lifecycle. This helps maintain focus on what’s most important . Prioritization can guide where to allocate resources and effort, especially when under constraints.
Step 5: Update as Necessary
Finally, regularly revisit the MoSCoW categorization , especially after major milestones or significant changes in the project environment. Also, be prepared to adjust the priorities in response to new information, stakeholder feedback, or changes in the external environment.
Implementing the MoSCoW Method is an exercise in strategic planning and adaptive management. It begins with a comprehensive gathering of project requirements, engaging a broad spectrum of stakeholders to ensure a multifaceted view of the project’s needs. The heart of the process lies in the collaborative categorization of these requirements, balancing differing perspectives to establish a shared priority framework.
As the project progresses, this method serves as a dynamic guide, directing resources and decision-making effectively. Regularly revisiting and adjusting these priorities ensures the project stays aligned with evolving objectives and constraints, making MoSCoW an indispensable tool for successful project management.
- Kuhn, J., 2009. Decrypting the MoSCoW analysis. The workable, practical guide to Do IT Yourself , 5 .
- Ahmad, K.S., Ahmad, N., Tahir, H. and Khan, S., 2017, July. Fuzzy_MoSCoW: A fuzzy based MoSCoW method for the prioritization of software requirements. In 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT) (pp. 433-437). IEEE.
Q: What types of projects is the MoSCoW method best suited for?
A: The MoSCoW method is versatile and can be used for various types of projects, ranging from software development and website redesign to manufacturing and logistics. It’s particularly useful for projects with multiple stakeholders and those that require a clear understanding of task priority.
Q: How often should the MoSCoW list be reviewed and updated?
A: The frequency of reviewing the MoSCoW list depends on the project’s complexity and how often its circumstances change. For fast-paced projects, a weekly or bi-weekly review might be necessary. For more stable projects, a monthly review could suffice.
Q: Can the MoSCoW method be integrated with other project management techniques?
A: Absolutely! The MoSCoW method can be used in conjunction with other project management methodologies like Agile, Scrum, or Lean Six Sigma. It serves as a prioritization tool that can easily be incorporated into other frameworks to make them even more effective.
Q: What should I do if stakeholders disagree on the categorization of tasks?
A: If there’s disagreement on task categorization, it’s useful to have a facilitated discussion to reach a consensus. You can also use a weighted scoring system to quantitatively assess each task’s importance, which can help in making more objective decisions.
Q: Are there any tools or software that can help in applying the MoSCoW method?
A: While the MoSCoW method can be applied using simple tools like whiteboards and Post-It notes, there are also specialized project management software that offer built-in MoSCoW categorization features. These tools can be particularly helpful for larger or more complex projects.

Daniel Croft
Daniel Croft is a seasoned continuous improvement manager with a Black Belt in Lean Six Sigma. With over 10 years of real-world application experience across diverse sectors, Daniel has a passion for optimizing processes and fostering a culture of efficiency. He's not just a practitioner but also an avid learner, constantly seeking to expand his knowledge. Outside of his professional life, Daniel has a keen Investing, statistics and knowledge-sharing, which led him to create the website www.learnleansigma.com, a platform dedicated to Lean Six Sigma and process improvement insights.

Free Lean Six Sigma Templates
Improve your Lean Six Sigma projects with our free templates. They're designed to make implementation and management easier, helping you achieve better results.
Was this helpful?

IMAGES
COMMENTS
I cancelled out the initial kinetic energy because: KE i = ½ mv f2. KE i = (½) (3.5) (0 2) = 0 J. I cancelled out the final potential energy because: PE f = mgh f. PE f = (3.5) (9.8) (0) = 0 J. (Note: In many of these problems I could cancel out mass but did not since it was provided) Since I did not cancel out mass I could answer the ...
Assume that no energy is lost to friction. At any point in the ride, the total mechanical energy is the same, and it is equal to the energy the car had at the top of the first rise. This is a result of the law of conservation of energy, which says that, in a closed system, total energy is conserved—that is, it is constant. Using subscripts 1 ...
Determine Ima's kinetic energy at the top of the loop. b. Determine Ima's potential energy at the top of the loop. c. Assuming negligible losses of energy due to friction and air resistance, determine Ima's total mechanical energy at the bottom of the loop (h=0 m). d. Determine Ima's speed at the bottom of the loop. Audio Guided Solution
Problem Set WE8: Total Mechanical Energy. Use mass, speed, and height values to calculate the total amount of mechancial energy possessed by an object. Includes 5 problems. Problem Set WE9: Work and Kinetic Energy 1. Use the work-energy theorem to calculate either the work or the kinetic energy. All problems are highly scaffolded.
How to Calculate Total Mechanical Energy. Step 1: Read the problem and identify all variables given within the problem as well as all forms of energy. Step 2: Using the equation for total ...
Solving for different variables using the Total Mechanical Energy equation using algebra.
Lesson 41: Total Mechanical Energy. A large number of questions you will do involve the Total Mechanical Energy of a system. Total mechanical energy is just the kinetic plus potential energy. As long as there are no outside forces unaccounted for, we know that the totals before and after will be equal. E k + E p = E k ' + E p '.
At maximum height, (the final position) the kinetic energy is. Kf = ½ mvf2 = ½ (1. 50 kg) (16. 6 m/s) 2 = 206 J. In this problem there are only conservative forces (namely, gravity). The mechanical energy is conserved: Ki + Ui = Kf + Uf. We already found the initial kinetic energy of the snowball: Ki = 300 J.
Answer: When mechanical energy is conserved in a system (no non-conservative forces like friction), the total energy at the beginning is equal to the total energy at the end. This principle allows us to relate the potential and kinetic energies at different points in time, simplifying the problem-solving process.
Energy Problem Solving. Consider the inclined plane problem that was just worked, but add a spring at the bottom of the incline. The spring will be compressed a distance Δx and then released. Find the velocity of the box when it rises back to where it was first compressed a height of Δh.
Conservation of Energy in general. Throughout the first half of the 19^\text {th} 19th century, engineers realized that thermal heat was another form of energy, capable of mechanical work. By 1850, the law of conservation of energy was formally stated for the first time, as the first law of thermodynamics.
The subscripts 2 and 1 indicate the final and initial velocity, respectively. This theorem was proposed and successfully tested by James Joule, shown in Figure 9.2.. Does the name Joule sound familiar? The joule (J) is the metric unit of measurement for both work and energy. The measurement of work and energy with the same unit reinforces the idea that work and energy are related and can be ...
We found the speed directly from the conservation of mechanical energy, without having to solve the differential equation for the motion of a pendulum (see Oscillations). We can approach this problem in terms of bar graphs of total energy. Initially, the particle has all potential energy, being at the highest point, and no kinetic energy.
The total mechanical energy of Lee Ben Fardest is the sum of the potential and kinetic energies. The two forms of energy sum up to 50 000 Joules. Notice also that the total mechanical energy of Lee Ben Fardest is a constant value throughout his motion. There are conditions under which the total mechanical energy will be a constant value and ...
A body of mass 0.5 kg is hanging at the end of a spring with an original length of 0.3 m. The increase in the length due to the body is 0.1m. Find out the total mechanical energy if the spring ...
Example Problem 1 - Solving Conservation of Energy Problems. ... Therefore, it has gained 0.33 Joules of kinetic energy because the total mechanical energy was conserved. Since is started with ...
Total mechanical energy is useful in solving problems because it allows us to analyze the motion of an object by considering its energy instead of individual forces. By using the conservation of energy principle, we can solve for unknown variables, such as velocity or height, without needing to know the specific forces acting on the object.
Trump took the stage later than expected at his Friday night rally in Bozeman, Montana, after a mechanical problem forced his plane to divert 140 miles east to Billings. The plane landed without ...
Meaning and acronym of the MoSCoW Method. Moscow is an acronym made up of the first letters. The two Os have been added to make the word 'moscow' readable, they don't have any meaning themselves. The M stands for 'Must haves', S for 'Should haves', C for 'Could haves' and W for 'Won't haves' or 'Would haves'. Figure ...
Work, Energy and Power: Problem Set Overview There are 20 ready-to-use problem sets on the topic of Work, Energy, and Power. The problems target your ability to use equations related to work and power, to calculate the kinetic, potential and total mechanical energy, and to use the work-energy relationship in order to determine the final speed, stopping distance or final height of an object.
The MoSCoW method is a simple and highly useful approach that enables you to prioritize project tasks as critical and non-critical. MoSCoW stands for: Must - These are tasks that you must complete for the project to be considered a success. Should - These are critical activities that are less urgent than Must tasks.
The MoSCoW Method is a prioritization tool that helps professionals in managing their time and effort.. To do so, it proposes to classify the importance of the different characteristics of a product (or a Project) according to their importance. Its name is an acronym of the 4 Prioritization Categories proposed (adding two "o"):. M ust Have.; S hould Have.; C ould Have.
Step 1: Gather Requirements. The first step in the MoSCoW method requires gathering a list of the tasks, activities, features, or requirements you need to prioritize in your project. For this step, you should engage with all relevant stakeholders, including project sponsors, end-users, and technical teams. This ensures that the requirements ...