1.1 Real Numbers: Algebra Essentials
Learning objectives.
In this section, you will:
- Classify a real number as a natural, whole, integer, rational, or irrational number.
- Perform calculations using order of operations.
- Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
- Evaluate algebraic expressions.
- Simplify algebraic expressions.
It is often said that mathematics is the language of science. If this is true, then an essential part of the language of mathematics is numbers. The earliest use of numbers occurred 100 centuries ago in the Middle East to count, or enumerate items. Farmers, cattle herders, and traders used tokens, stones, or markers to signify a single quantity—a sheaf of grain, a head of livestock, or a fixed length of cloth, for example. Doing so made commerce possible, leading to improved communications and the spread of civilization.
Three to four thousand years ago, Egyptians introduced fractions. They first used them to show reciprocals. Later, they used them to represent the amount when a quantity was divided into equal parts.
But what if there were no cattle to trade or an entire crop of grain was lost in a flood? How could someone indicate the existence of nothing? From earliest times, people had thought of a “base state” while counting and used various symbols to represent this null condition. However, it was not until about the fifth century CE in India that zero was added to the number system and used as a numeral in calculations.
Clearly, there was also a need for numbers to represent loss or debt. In India, in the seventh century CE, negative numbers were used as solutions to mathematical equations and commercial debts. The opposites of the counting numbers expanded the number system even further.
Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.

Classifying a Real Number
The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as { 1 , 2 , 3 , ... } { 1 , 2 , 3 , ... } where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .
The set of integers adds the opposites of the natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.
The set of rational numbers is written as { m n | m and n are integers and n ≠ 0 } . { m n | m and n are integers and n ≠ 0 } . Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.
Because they are fractions, any rational number can also be expressed as a terminating or repeating decimal. Any rational number can be represented as either:
- ⓐ a terminating decimal: 15 8 = 1.875 , 15 8 = 1.875 , or
- ⓑ a repeating decimal: 4 11 = 0.36363636 … = 0. 36 ¯ 4 11 = 0.36363636 … = 0. 36 ¯
We use a line drawn over the repeating block of numbers instead of writing the group multiple times.
Writing Integers as Rational Numbers
Write each of the following as a rational number.
Write a fraction with the integer in the numerator and 1 in the denominator.
- ⓐ 7 = 7 1 7 = 7 1
- ⓑ 0 = 0 1 0 = 0 1
- ⓒ −8 = − 8 1 −8 = − 8 1
Identifying Rational Numbers
Write each of the following rational numbers as either a terminating or repeating decimal.
- ⓐ − 5 7 − 5 7
- ⓑ 15 5 15 5
- ⓒ 13 25 13 25
Write each fraction as a decimal by dividing the numerator by the denominator.
- ⓐ − 5 7 = −0. 714285 ——— , − 5 7 = −0. 714285 ——— , a repeating decimal
- ⓑ 15 5 = 3 15 5 = 3 (or 3.0), a terminating decimal
- ⓒ 13 25 = 0.52 , 13 25 = 0.52 , a terminating decimal
- ⓐ 68 17 68 17
- ⓑ 8 13 8 13
- ⓒ − 17 20 − 17 20
Irrational Numbers
At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even 3 2 , 3 2 , but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.
Differentiating Rational and Irrational Numbers
Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.
- ⓑ 33 9 33 9
- ⓓ 17 34 17 34
- ⓔ 0.3033033303333 … 0.3033033303333 …
- ⓐ 25 : 25 : This can be simplified as 25 = 5. 25 = 5. Therefore, 25 25 is rational.
So, 33 9 33 9 is rational and a repeating decimal.
- ⓒ 11 : 11 11 : 11 is irrational because 11 is not a perfect square and 11 11 cannot be expressed as a fraction.
So, 17 34 17 34 is rational and a terminating decimal.
- ⓔ 0.3033033303333 … 0.3033033303333 … is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
- ⓐ 7 77 7 77
- ⓒ 4.27027002700027 … 4.27027002700027 …
- ⓓ 91 13 91 13
Real Numbers
Given any number n , we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers . As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.
The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure 1 .
Classifying Real Numbers
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?
- ⓐ − 10 3 − 10 3
- ⓒ − 289 − 289
- ⓓ −6 π −6 π
- ⓔ 0.615384615384 … 0.615384615384 …
- ⓐ − 10 3 − 10 3 is negative and rational. It lies to the left of 0 on the number line.
- ⓑ 5 5 is positive and irrational. It lies to the right of 0.
- ⓒ − 289 = − 17 2 = −17 − 289 = − 17 2 = −17 is negative and rational. It lies to the left of 0.
- ⓓ −6 π −6 π is negative and irrational. It lies to the left of 0.
- ⓔ 0.615384615384 … 0.615384615384 … is a repeating decimal so it is rational and positive. It lies to the right of 0.
- ⓑ −11.411411411 … −11.411411411 …
- ⓒ 47 19 47 19
- ⓓ − 5 2 − 5 2
- ⓔ 6.210735 6.210735
Sets of Numbers as Subsets
Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure 2 .
Sets of Numbers
The set of natural numbers includes the numbers used for counting: { 1 , 2 , 3 , ... } . { 1 , 2 , 3 , ... } .
The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .
The set of integers adds the negative natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } .
The set of rational numbers includes fractions written as { m n | m and n are integers and n ≠ 0 } . { m n | m and n are integers and n ≠ 0 } .
The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: { h | h is not a rational number } . { h | h is not a rational number } .
Differentiating the Sets of Numbers
Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q′ ).
- ⓔ 3.2121121112 … 3.2121121112 …
| a. | X | X | X | X | |
| b. | X | ||||
| c. | X | ||||
| d. –6 | X | X | |||
| e. 3.2121121112... | X |
- ⓐ − 35 7 − 35 7
- ⓔ 4.763763763 … 4.763763763 …
Performing Calculations Using the Order of Operations
When we multiply a number by itself, we square it or raise it to a power of 2. For example, 4 2 = 4 ⋅ 4 = 16. 4 2 = 4 ⋅ 4 = 16. We can raise any number to any power. In general, the exponential notation a n a n means that the number or variable a a is used as a factor n n times.
In this notation, a n a n is read as the n th power of a , a , or a a to the n n where a a is called the base and n n is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, 24 + 6 ⋅ 2 3 − 4 2 24 + 6 ⋅ 2 3 − 4 2 is a mathematical expression.
To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations . This is a sequence of rules for evaluating such expressions.
Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.
The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.
Let’s take a look at the expression provided.
There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify 4 2 4 2 as 16.
Next, perform multiplication or division, left to right.
Lastly, perform addition or subtraction, left to right.
Therefore, 24 + 6 ⋅ 2 3 − 4 2 = 12. 24 + 6 ⋅ 2 3 − 4 2 = 12.
For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.
Order of Operations
Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :
P (arentheses) E (xponents) M (ultiplication) and D (ivision) A (ddition) and S (ubtraction)
Given a mathematical expression, simplify it using the order of operations.
- Step 1. Simplify any expressions within grouping symbols.
- Step 2. Simplify any expressions containing exponents or radicals.
- Step 3. Perform any multiplication and division in order, from left to right.
- Step 4. Perform any addition and subtraction in order, from left to right.
Using the Order of Operations
Use the order of operations to evaluate each of the following expressions.
- ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 )
- ⓑ 5 2 − 4 7 − 11 − 2 5 2 − 4 7 − 11 − 2
- ⓒ 6 − | 5 − 8 | + 3 ( 4 − 1 ) 6 − | 5 − 8 | + 3 ( 4 − 1 )
- ⓓ 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2
- ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1
- ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction. ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction.
Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.
- ⓒ 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition. 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition.
In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.
- ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add. 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add.
- ⓐ 5 2 − 4 2 + 7 ( 5 − 4 ) 2 5 2 − 4 2 + 7 ( 5 − 4 ) 2
- ⓑ 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6
- ⓒ | 1.8 − 4.3 | + 0.4 15 + 10 | 1.8 − 4.3 | + 0.4 15 + 10
- ⓓ 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2
- ⓔ [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 ) [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 )
Using Properties of Real Numbers
For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.
Commutative Properties
The commutative property of addition states that numbers may be added in any order without affecting the sum.
We can better see this relationship when using real numbers.
Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.
Again, consider an example with real numbers.
It is important to note that neither subtraction nor division is commutative. For example, 17 − 5 17 − 5 is not the same as 5 − 17. 5 − 17. Similarly, 20 ÷ 5 ≠ 5 ÷ 20. 20 ÷ 5 ≠ 5 ÷ 20.
Associative Properties
The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.
Consider this example.
The associative property of addition tells us that numbers may be grouped differently without affecting the sum.
This property can be especially helpful when dealing with negative integers. Consider this example.
Are subtraction and division associative? Review these examples.
As we can see, neither subtraction nor division is associative.
Distributive Property
The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.
This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
A special case of the distributive property occurs when a sum of terms is subtracted.
For example, consider the difference 12 − ( 5 + 3 ) . 12 − ( 5 + 3 ) . We can rewrite the difference of the two terms 12 and ( 5 + 3 ) ( 5 + 3 ) by turning the subtraction expression into addition of the opposite. So instead of subtracting ( 5 + 3 ) , ( 5 + 3 ) , we add the opposite.
Now, distribute −1 −1 and simplify the result.
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.
The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.
For example, we have ( −6 ) + 0 = −6 ( −6 ) + 0 = −6 and 23 ⋅ 1 = 23. 23 ⋅ 1 = 23. There are no exceptions for these properties; they work for every real number, including 0 and 1.
Inverse Properties
The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted by (− a ), that, when added to the original number, results in the additive identity, 0.
For example, if a = −8 , a = −8 , the additive inverse is 8, since ( −8 ) + 8 = 0. ( −8 ) + 8 = 0.
The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted 1 a , 1 a , that, when multiplied by the original number, results in the multiplicative identity, 1.
For example, if a = − 2 3 , a = − 2 3 , the reciprocal, denoted 1 a , 1 a , is − 3 2 − 3 2 because
Properties of Real Numbers
The following properties hold for real numbers a , b , and c .
| Addition | Multiplication | |
|---|---|---|
| There exists a unique real number called the additive identity, 0, such that, for any real number | There exists a unique real number called the multiplicative identity, 1, such that, for any real number | |
| Every real number a has an additive inverse, or opposite, denoted , such that | Every nonzero real number has a multiplicative inverse, or reciprocal, denoted such that | |
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- ⓐ 3 ⋅ 6 + 3 ⋅ 4 3 ⋅ 6 + 3 ⋅ 4
- ⓑ ( 5 + 8 ) + ( −8 ) ( 5 + 8 ) + ( −8 )
- ⓒ 6 − ( 15 + 9 ) 6 − ( 15 + 9 )
- ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) 4 7 ⋅ ( 2 3 ⋅ 7 4 )
- ⓔ 100 ⋅ [ 0.75 + ( −2.38 ) ] 100 ⋅ [ 0.75 + ( −2.38 ) ]
- ⓐ 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify. 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify.
- ⓑ ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition. ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition.
- ⓒ 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify. 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify.
- ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication. 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication.
- ⓔ 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify. 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify.
- ⓐ ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ] ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ]
- ⓑ 5 ⋅ ( 6.2 + 0.4 ) 5 ⋅ ( 6.2 + 0.4 )
- ⓒ 18 − ( 7 −15 ) 18 − ( 7 −15 )
- ⓓ 17 18 + [ 4 9 + ( − 17 18 ) ] 17 18 + [ 4 9 + ( − 17 18 ) ]
- ⓔ 6 ⋅ ( −3 ) + 6 ⋅ 3 6 ⋅ ( −3 ) + 6 ⋅ 3
Evaluating Algebraic Expressions
So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as x + 5 , 4 3 π r 3 , x + 5 , 4 3 π r 3 , or 2 m 3 n 2 . 2 m 3 n 2 . In the expression x + 5 , x + 5 , 5 is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.
In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.
Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.
Describing Algebraic Expressions
List the constants and variables for each algebraic expression.
- ⓑ 4 3 π r 3 4 3 π r 3
- ⓒ 2 m 3 n 2 2 m 3 n 2
| Constants | Variables | |
|---|---|---|
| a. + 5 | 5 | |
| b. | ||
| c. | 2 |
- ⓐ 2 π r ( r + h ) 2 π r ( r + h )
- ⓑ 2( L + W )
- ⓒ 4 y 3 + y 4 y 3 + y
Evaluating an Algebraic Expression at Different Values
Evaluate the expression 2 x − 7 2 x − 7 for each value for x.
- ⓐ x = 0 x = 0
- ⓑ x = 1 x = 1
- ⓒ x = 1 2 x = 1 2
- ⓓ x = −4 x = −4
- ⓐ Substitute 0 for x . x . 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7
- ⓑ Substitute 1 for x . x . 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5
- ⓒ Substitute 1 2 1 2 for x . x . 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6
- ⓓ Substitute −4 −4 for x . x . 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15
Evaluate the expression 11 − 3 y 11 − 3 y for each value for y.
- ⓐ y = 2 y = 2
- ⓑ y = 0 y = 0
- ⓒ y = 2 3 y = 2 3
- ⓓ y = −5 y = −5
Evaluate each expression for the given values.
- ⓐ x + 5 x + 5 for x = −5 x = −5
- ⓑ t 2 t −1 t 2 t −1 for t = 10 t = 10
- ⓒ 4 3 π r 3 4 3 π r 3 for r = 5 r = 5
- ⓓ a + a b + b a + a b + b for a = 11 , b = −8 a = 11 , b = −8
- ⓔ 2 m 3 n 2 2 m 3 n 2 for m = 2 , n = 3 m = 2 , n = 3
- ⓐ Substitute −5 −5 for x . x . x + 5 = ( −5 ) + 5 = 0 x + 5 = ( −5 ) + 5 = 0
- ⓑ Substitute 10 for t . t . t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19 t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19
- ⓒ Substitute 5 for r . r . 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π
- ⓓ Substitute 11 for a a and –8 for b . b . a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85 a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85
- ⓔ Substitute 2 for m m and 3 for n . n . 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12
- ⓐ y + 3 y − 3 y + 3 y − 3 for y = 5 y = 5
- ⓑ 7 − 2 t 7 − 2 t for t = −2 t = −2
- ⓒ 1 3 π r 2 1 3 π r 2 for r = 11 r = 11
- ⓓ ( p 2 q ) 3 ( p 2 q ) 3 for p = −2 , q = 3 p = −2 , q = 3
- ⓔ 4 ( m − n ) − 5 ( n − m ) 4 ( m − n ) − 5 ( n − m ) for m = 2 3 , n = 1 3 m = 2 3 , n = 1 3
An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation 2 x + 1 = 7 2 x + 1 = 7 has the solution of 3 because when we substitute 3 for x x in the equation, we obtain the true statement 2 ( 3 ) + 1 = 7. 2 ( 3 ) + 1 = 7.
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area A A of a circle in terms of the radius r r of the circle: A = π r 2 . A = π r 2 . For any value of r , r , the area A A can be found by evaluating the expression π r 2 . π r 2 .
Using a Formula
A right circular cylinder with radius r r and height h h has the surface area S S (in square units) given by the formula S = 2 π r ( r + h ) . S = 2 π r ( r + h ) . See Figure 3 . Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of π . π .
Evaluate the expression 2 π r ( r + h ) 2 π r ( r + h ) for r = 6 r = 6 and h = 9. h = 9.
The surface area is 180 π 180 π square inches.
A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be A = ( L + 16 ) ( W + 16 ) − L ⋅ W . A = ( L + 16 ) ( W + 16 ) − L ⋅ W . See Figure 4 . Find the area of a mat for a photograph with length 32 cm and width 24 cm.
Simplifying Algebraic Expressions
Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.
Simplify each algebraic expression.
- ⓐ 3 x − 2 y + x − 3 y − 7 3 x − 2 y + x − 3 y − 7
- ⓑ 2 r − 5 ( 3 − r ) + 4 2 r − 5 ( 3 − r ) + 4
- ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) ( 4 t − 5 4 s ) − ( 2 3 t + 2 s )
- ⓓ 2 m n − 5 m + 3 m n + n 2 m n − 5 m + 3 m n + n
- ⓐ 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify. 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify.
- ⓑ 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify. 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify.
- ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify. ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify.
- ⓓ 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify. 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify.
- ⓐ 2 3 y − 2 ( 4 3 y + z ) 2 3 y − 2 ( 4 3 y + z )
- ⓑ 5 t − 2 − 3 t + 1 5 t − 2 − 3 t + 1
- ⓒ 4 p ( q − 1 ) + q ( 1 − p ) 4 p ( q − 1 ) + q ( 1 − p )
- ⓓ 9 r − ( s + 2 r ) + ( 6 − s ) 9 r − ( s + 2 r ) + ( 6 − s )
Simplifying a Formula
A rectangle with length L L and width W W has a perimeter P P given by P = L + W + L + W . P = L + W + L + W . Simplify this expression.
If the amount P P is deposited into an account paying simple interest r r for time t , t , the total value of the deposit A A is given by A = P + P r t . A = P + P r t . Simplify the expression. (This formula will be explored in more detail later in the course.)
Access these online resources for additional instruction and practice with real numbers.
- Simplify an Expression.
- Evaluate an Expression 1.
- Evaluate an Expression 2.
1.1 Section Exercises
Is 2 2 an example of a rational terminating, rational repeating, or irrational number? Tell why it fits that category.
What is the order of operations? What acronym is used to describe the order of operations, and what does it stand for?
What do the Associative Properties allow us to do when following the order of operations? Explain your answer.
For the following exercises, simplify the given expression.
10 + 2 × ( 5 − 3 ) 10 + 2 × ( 5 − 3 )
6 ÷ 2 − ( 81 ÷ 3 2 ) 6 ÷ 2 − ( 81 ÷ 3 2 )
18 + ( 6 − 8 ) 3 18 + ( 6 − 8 ) 3
−2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2 −2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2
4 − 6 + 2 × 7 4 − 6 + 2 × 7
3 ( 5 − 8 ) 3 ( 5 − 8 )
4 + 6 − 10 ÷ 2 4 + 6 − 10 ÷ 2
12 ÷ ( 36 ÷ 9 ) + 6 12 ÷ ( 36 ÷ 9 ) + 6
( 4 + 5 ) 2 ÷ 3 ( 4 + 5 ) 2 ÷ 3
3 − 12 × 2 + 19 3 − 12 × 2 + 19
2 + 8 × 7 ÷ 4 2 + 8 × 7 ÷ 4
5 + ( 6 + 4 ) − 11 5 + ( 6 + 4 ) − 11
9 − 18 ÷ 3 2 9 − 18 ÷ 3 2
14 × 3 ÷ 7 − 6 14 × 3 ÷ 7 − 6
9 − ( 3 + 11 ) × 2 9 − ( 3 + 11 ) × 2
6 + 2 × 2 − 1 6 + 2 × 2 − 1
64 ÷ ( 8 + 4 × 2 ) 64 ÷ ( 8 + 4 × 2 )
9 + 4 ( 2 2 ) 9 + 4 ( 2 2 )
( 12 ÷ 3 × 3 ) 2 ( 12 ÷ 3 × 3 ) 2
25 ÷ 5 2 − 7 25 ÷ 5 2 − 7
( 15 − 7 ) × ( 3 − 7 ) ( 15 − 7 ) × ( 3 − 7 )
2 × 4 − 9 ( −1 ) 2 × 4 − 9 ( −1 )
4 2 − 25 × 1 5 4 2 − 25 × 1 5
12 ( 3 − 1 ) ÷ 6 12 ( 3 − 1 ) ÷ 6
For the following exercises, evaluate the expression using the given value of the variable.
8 ( x + 3 ) – 64 8 ( x + 3 ) – 64 for x = 2 x = 2
4 y + 8 – 2 y 4 y + 8 – 2 y for y = 3 y = 3
( 11 a + 3 ) − 18 a + 4 ( 11 a + 3 ) − 18 a + 4 for a = –2 a = –2
4 z − 2 z ( 1 + 4 ) – 36 4 z − 2 z ( 1 + 4 ) – 36 for z = 5 z = 5
4 y ( 7 − 2 ) 2 + 200 4 y ( 7 − 2 ) 2 + 200 for y = –2 y = –2
− ( 2 x ) 2 + 1 + 3 − ( 2 x ) 2 + 1 + 3 for x = 2 x = 2
For the 8 ( 2 + 4 ) − 15 b + b 8 ( 2 + 4 ) − 15 b + b for b = –3 b = –3
2 ( 11 c − 4 ) – 36 2 ( 11 c − 4 ) – 36 for c = 0 c = 0
4 ( 3 − 1 ) x – 4 4 ( 3 − 1 ) x – 4 for x = 10 x = 10
1 4 ( 8 w − 4 2 ) 1 4 ( 8 w − 4 2 ) for w = 1 w = 1
For the following exercises, simplify the expression.
4 x + x ( 13 − 7 ) 4 x + x ( 13 − 7 )
2 y − ( 4 ) 2 y − 11 2 y − ( 4 ) 2 y − 11
a 2 3 ( 64 ) − 12 a ÷ 6 a 2 3 ( 64 ) − 12 a ÷ 6
8 b − 4 b ( 3 ) + 1 8 b − 4 b ( 3 ) + 1
5 l ÷ 3 l × ( 9 − 6 ) 5 l ÷ 3 l × ( 9 − 6 )
7 z − 3 + z × 6 2 7 z − 3 + z × 6 2
4 × 3 + 18 x ÷ 9 − 12 4 × 3 + 18 x ÷ 9 − 12
9 ( y + 8 ) − 27 9 ( y + 8 ) − 27
( 9 6 t − 4 ) 2 ( 9 6 t − 4 ) 2
6 + 12 b − 3 × 6 b 6 + 12 b − 3 × 6 b
18 y − 2 ( 1 + 7 y ) 18 y − 2 ( 1 + 7 y )
( 4 9 ) 2 × 27 x ( 4 9 ) 2 × 27 x
8 ( 3 − m ) + 1 ( − 8 ) 8 ( 3 − m ) + 1 ( − 8 )
9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x ) 9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x )
5 2 − 4 ( 3 x ) 5 2 − 4 ( 3 x )
Real-World Applications
For the following exercises, consider this scenario: Fred earns $40 at the community garden. He spends $10 on a streaming subscription, puts half of what is left in a savings account, and gets another $5 for walking his neighbor’s dog.
Write the expression that represents the number of dollars Fred keeps (and does not put in his savings account). Remember the order of operations.
How much money does Fred keep?
For the following exercises, solve the given problem.
According to the U.S. Mint, the diameter of a quarter is 0.955 inches. The circumference of the quarter would be the diameter multiplied by π . π . Is the circumference of a quarter a whole number, a rational number, or an irrational number?
Jessica and her roommate, Adriana, have decided to share a change jar for joint expenses. Jessica put her loose change in the jar first, and then Adriana put her change in the jar. We know that it does not matter in which order the change was added to the jar. What property of addition describes this fact?
For the following exercises, consider this scenario: There is a mound of g g pounds of gravel in a quarry. Throughout the day, 400 pounds of gravel is added to the mound. Two orders of 600 pounds are sold and the gravel is removed from the mound. At the end of the day, the mound has 1,200 pounds of gravel.
Write the equation that describes the situation.
Solve for g .
For the following exercise, solve the given problem.
Ramon runs the marketing department at their company. Their department gets a budget every year, and every year, they must spend the entire budget without going over. If they spend less than the budget, then the department gets a smaller budget the following year. At the beginning of this year, Ramon got $2.5 million for the annual marketing budget. They must spend the budget such that 2,500,000 − x = 0. 2,500,000 − x = 0. What property of addition tells us what the value of x must be?
For the following exercises, use a graphing calculator to solve for x . Round the answers to the nearest hundredth.
0.5 ( 12.3 ) 2 − 48 x = 3 5 0.5 ( 12.3 ) 2 − 48 x = 3 5
( 0.25 − 0.75 ) 2 x − 7.2 = 9.9 ( 0.25 − 0.75 ) 2 x − 7.2 = 9.9
If a whole number is not a natural number, what must the number be?
Determine whether the statement is true or false: The multiplicative inverse of a rational number is also rational.
Determine whether the statement is true or false: The product of a rational and irrational number is always irrational.
Determine whether the simplified expression is rational or irrational: −18 − 4 ( 5 ) ( −1 ) . −18 − 4 ( 5 ) ( −1 ) .
Determine whether the simplified expression is rational or irrational: −16 + 4 ( 5 ) + 5 . −16 + 4 ( 5 ) + 5 .
The division of two natural numbers will always result in what type of number?
What property of real numbers would simplify the following expression: 4 + 7 ( x − 1 ) ? 4 + 7 ( x − 1 ) ?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/1-1-real-numbers-algebra-essentials
© Jun 28, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Math by the Mountain
Teaching secondary mathematics in the pacific northwest, how i teach the real number system, classifying real numbers, and closure.
This is part of my Unit 1 Interactive Notebook for Algebra 1. You can view the rest of it here .
1.1 – The Real Number System, Classifying Real Numbers & Closure
There’s nothing trickier than picking the very first topic to cover in all of Algebra 1. So many options, so what goes first?
To start the very first unit of Algebra 1 off, I begin by talking about the real number system and how we classify numbers.
Why oh why, is this where I start , you might ask?
Instilling this vocabulary is very important in helping students be able to hold fluent conversations about math. I can’t tell you how many students I’ve had in Algebra 2 (or Pre-Calc!) over the years that have asked “what’s an integer?” and they are unable to complete a problem that they otherwise would know how to do solely because they lack the basic vocabulary and don’t understand what the question is asking.

This is silly, and I want to prevent these things from happening as much as possible. Math really is its own language , and helping students learn it will allow them to be more confident and much more successful in the long run.

Next, I introduced my first flowchart of the year. I want to instill in students that their notebook is really a great reference, and that there are tools in there that are really meant to help them. We quickly filled out 3 flowchart examples, to show students how they can use this if they get stuck on their homework. ( Note: flowcharts are included in a separate bundle and are not part of the Unit 1 interactive notebook kit, which contains notes and warm-ups).
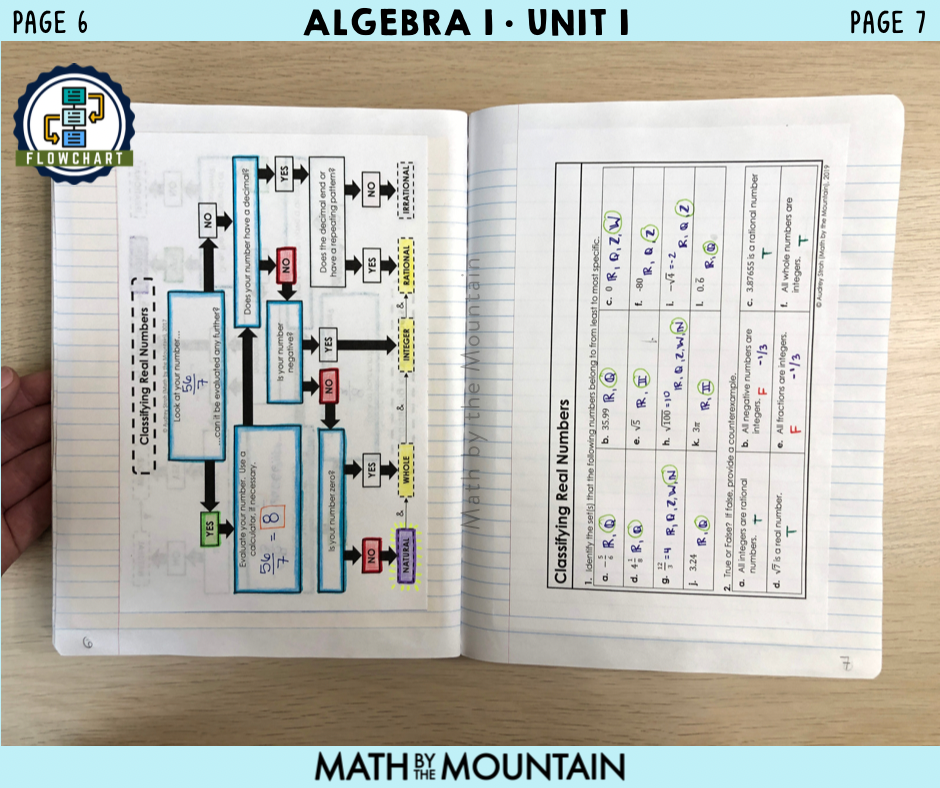
To finish off the class, I used the warm-up on Closure from my set of Unit 1 Warm-Ups as an exit slip. I don’t always have a special, topic-specific, pre-printed exit slip for my lessons because I often use these exit slip templates that I print off in mass quantities at the beginning of the year. That said, it’s really nice to have a formal exit slip for the first few experiences of the year.

Next day – I like to begin each day with a recap warm-up over the prior day’s lesson. Students work on the warm-up during the first 3-5 minutes of class and then students present solutions. Like the notes, this gets glued into their interactive notebook (INB) for quick reference. I love including the warm-ups because it is like the summary of the entire unit and students can quickly see examples.

This lesson is part of my Unit 1 Interactive Notebook for Algebra 1. You can view the rest of the unit here .
Like what you see? Grab the entire download-and-done unit!
What do all those symbols mean?

Pages marked with the “understanding” symbol provide special opportunities to slow down a topic and build conceptual understanding so you can speed up later and in the long run. These will be essential in developing your students’ understanding of what it is that they are doing and why .

Pages marked with the “flowchart” symbol are the perfect companion differentiation tool to help ensure that all students can find success. They are great study tools that students can refer back to over and over again and to turn to when they need help getting “un-stuck.” Use them to introduce a topic!

Pages marked with the “bonus file” symbol provide extra utility to the interactive notebook. Starting an interactive notebook can feel really daunting, but it doesn’t need to be. These pages are those “extras” that make an interactive notebook function all the better, and make your life easier, too!
These understanding builders are included in all Algebra 1 interactive notebook kits.
Flowcharts are not included in notebook kits and are sold separately here .
Bonus files are special to the mega bundle of all Algebra 1 notebook kits, sold here .
Share this:
One thought on “ how i teach the real number system, classifying real numbers, and closure ”.
- Pingback: Algebra 1 Unit 1 Interactive Notebook Pages – The Foundations of Algebra – Math by the Mountain
Leave a comment Cancel reply

- Already have a WordPress.com account? Log in now.
- Subscribe Subscribed
- Copy shortlink
- Report this content
- View post in Reader
- Manage subscriptions
- Collapse this bar
- Skip to main content
- Skip to primary sidebar
CLICK HERE TO LEARN ABOUT MTM ALL ACCESS MEMBERSHIP FOR GRADES 6-ALGEBRA 1
Maneuvering the Middle
Student-Centered Math Lessons
Teaching the Real Number System

The real number system can really confuse students. I will admit, at times, I felt confused too! Let’s check out 4 strategies that will help you teach classifying real numbers, and will help your students master the concept.

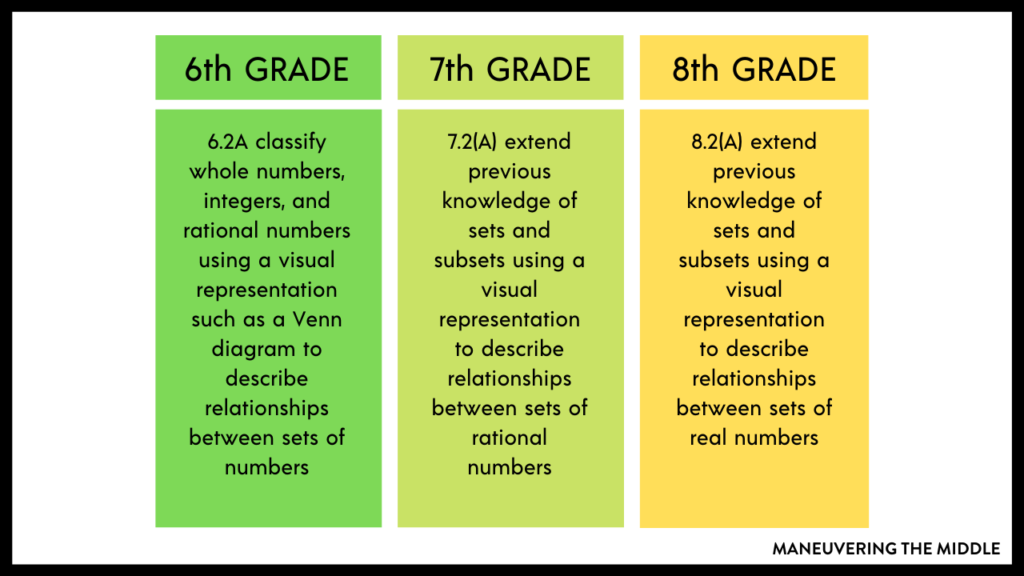
Vertical Alignment
Before we jump to that, let’s take a look at the standard and how it progresses through middle school, and then take a look at some STAAR test question examples. I have highlighted some helpful pieces.

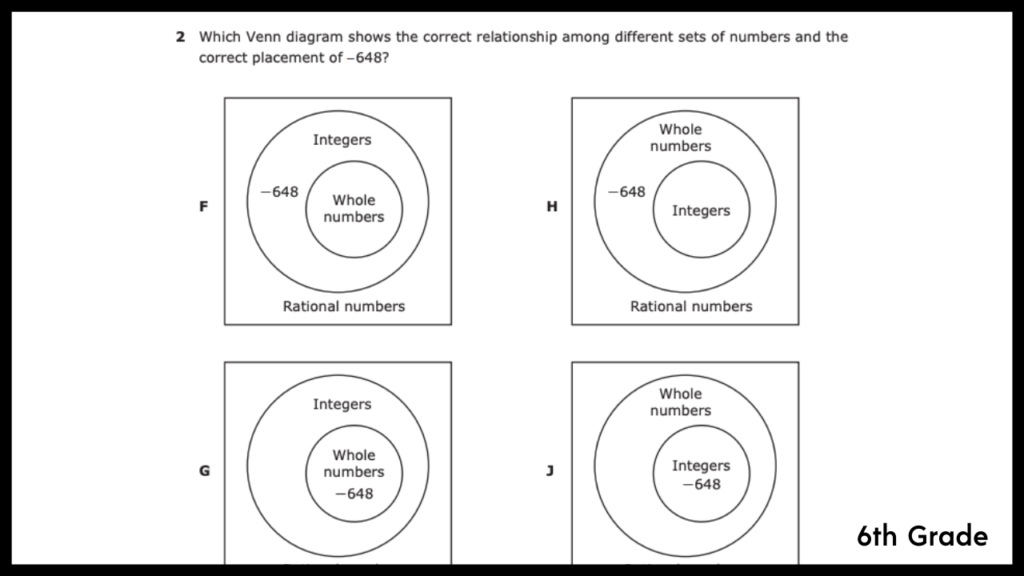
Real Number System Test Questions
Strategy #1 – Vocabulary
Vocabulary is crucial when teaching the real number system. Luckily, the content scaffolds by grade level.
- 6th Grade: whole, integer, rational
- 7th Grade: natural, whole, integer, rational
- 8th Grade: natural, whole, integer, rational, irrational
Since the progression of standards is pretty clear, each subsequent year a student must learn one brand new word. Although the vocabulary is important, I think students need to see examples more than they need to memorize the exact definition.
Bright idea! One way to push students’ learning is to ask them to come up with definitions based on observing numbers that have already been classified. Check out the example below.
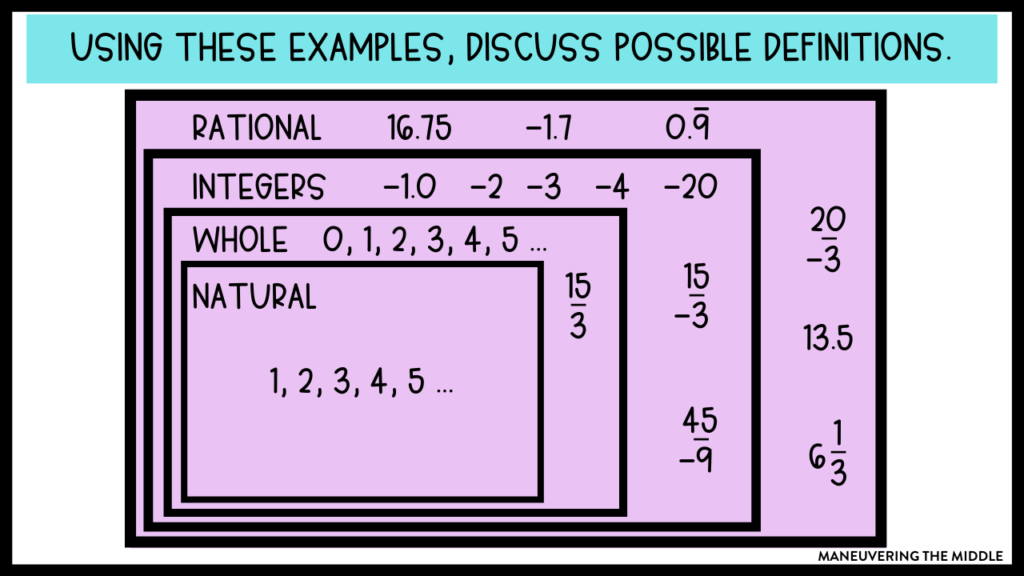
Some thought provoking questions might be:
- What differences do you see between the numbers inside integers and whole numbers?
- What is different about the fractions classified as whole numbers versus the fractions classified as rational numbers?
Strategy #2 – Visuals
Notice that in each grade level standard, the term “visual representation” is used. In addition, in each test question example, there is a venn diagram of sorts. This means that students will not be expected to classify a number in the real number system without a venn diagram present to guide them, so make sure you are modeling with one, and students are practicing with one.
Check out the one I made! Hint: Washi tape helps with straight lines. If you use Post-it Notes , the anchor chart can be interactive and reused each class period.

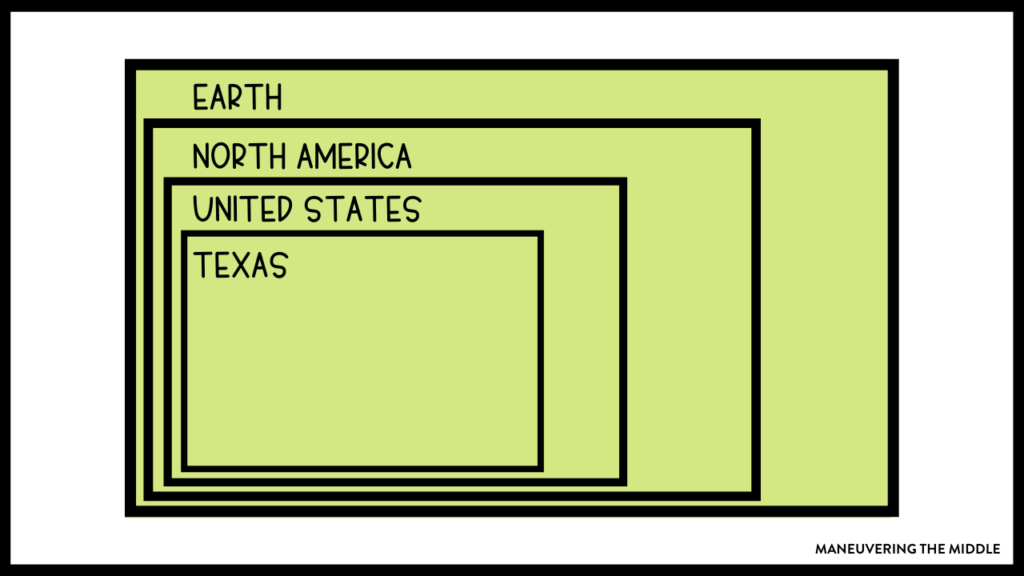
Students need to be taught how to use the venn diagram. Don’t assume (like me) that it is intuitive. I would start by using a similar venn diagram that is not related to math. You can steal this example if you would like. (Warning: You may be concerned about students’ geography if you use this example.)
You can ask these types of questions:
- If someone is from Texas, can you assume they are also from the United States?
- If someone lives in Oklahoma, where would you place them on the diagram?
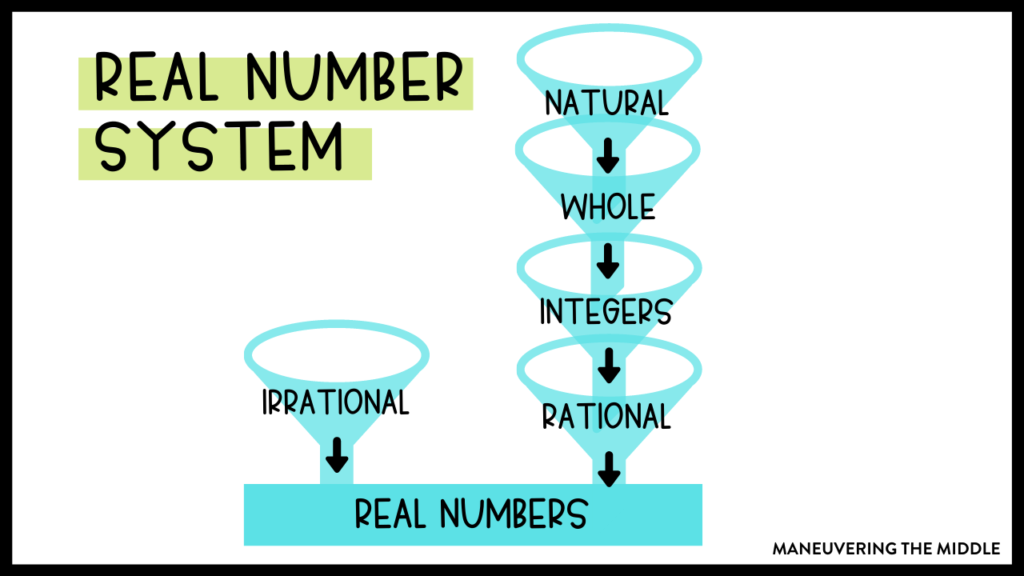
If students are struggling to use the venn diagram to understand the relationships between sets of numbers, then try exposing them to the funnel example. Using the number 17: 17 would be dropped into the natural number funnel thus falling through the whole, integer, rational, and real number funnels. The number -17 would be dropped into the integer funnel and thus continue into rational and real numbers. Then you would explain that -17 is an integer, a rational number, and a real number, but you typically call numbers by the funnel that it is dropped in.
Strategy #3 – Simplify Before You Classify
I saw this idea on a Middle School Math Facebook group, and it is so clever and catchy! Teach students to simplify before they classify in the real number system. Fractions like 16/4 are a great example of this. If students are familiar with the definition of rational numbers, they may think, “16/4 must only be a rational number because rational numbers are numbers that can be written as fractions.” That student is technically right, 16/4 is rational, but that is not all. If you teach students to simplify before you classify, a student would simplify this to 4, thus changing its classification.
You see this with square roots too. Many irrational number definitions include the phrase “square roots,” so a student might incorrectly classify the square root of 100 as irrational. Simplify before you classify!

Strategy #4 – Make It Interactive
Since this skill requires very little computation, this is an opportunity to engage students in something hands-on. Here is what I have done:
- Flyswatter Game (ideally after students have shown mastery, so they aren’t just swatting uncontrollably)
- Post-it Notes – have students write down a bunch of different types of numbers on individual Post-it Notes and then swap with a partner. Then they have to categorize the numbers from their partner.
- Grab a 6th grade or 8th grade activity bundle that includes classifying the real number activities.

Classifying numbers in the real number system can be really engaging. It also would provide a math-win for some of my struggling students. How do you make classifying numbers engaging?

Digital Math Activities
Check out these related products from my shop.

Classification of Real Numbers
How to classify real numbers.

The “stack of funnels” diagram below will help us easily classify any real numbers. But first, we need to describe what kinds of elements are included in each group of numbers. A funnel represents each group or set of numbers.

Description of Each Set of Real Numbers

Natural numbers (also known as counting numbers) are the numbers that we use to count. It begins with 1, then 2, 3, and so on.
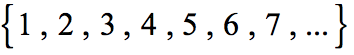
Whole numbers are a slight “upgrade” of the natural numbers because we simply add the element zero to the current set of natural numbers. Think of whole numbers as natural numbers together with zero.
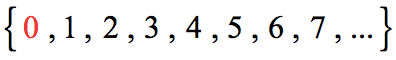
Integers include all whole numbers together with the “negatives” or opposites of the natural numbers.
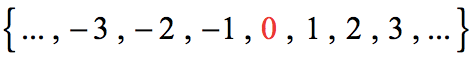
Rational numbers are numbers that can be expressed as a ratio of integers. That means if we can write a given number as a fraction where the numerator and denominator are both integers; then it is a rational number.
Symbolically, we can write a rational number as:
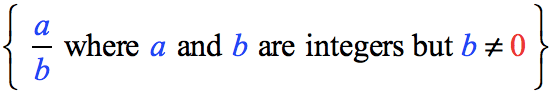
Caution: The denominator cannot equal zero.
Rational numbers can also appear in decimal form . If the decimal number either terminates or repeats, then it is possible to write it as a fraction with an integer numerator and denominator. Thus, it is rational as well.

Irrational numbers are all numbers that when written in decimal form do not repeat and do not terminate. In other words, it goes on forever indefinitely without having a definite pattern.
Real numbers include both rational and irrational numbers. Remember that under the set of rational numbers, we have the subcategories or subsets of integers, whole numbers, and natural numbers.
Hierarchical Format of Real Numbers
We can also express the subsets of the set of real numbers in a hierarchical presentation. This way, we can clearly see how the different sets are related and distinct.
- Real Numbers [latex]\mathbb{R}[/latex]
- 1.1.1.1.1 Natural Numbers [latex]\mathbb{N}[/latex]
- 1.2 Irrational Numbers
Classification of Real Numbers Examples
Example 1 : A natural number is also a whole number. ( True or False )
The set of whole numbers includes the number zero and all natural numbers. This is a true statement.
Example 2 : An integer is always a whole number. ( True or False )
The set of integers is composed of the number zero, natural numbers, and the “negatives” of natural numbers. That means some integers are whole numbers, but not all.
For instance, [latex] – 2[/latex] is an integer but not a whole number. This statement is false .
Example 3 : Every rational number is also an integer. ( True or False )
The word “every” means “all”. Can you think of a rational number that is not an integer? You only need one counterexample to show that this statement is false.
The fraction [latex]\Large{1 \over 2}[/latex] is an example of a rational number that is NOT an integer. So this statement is false .
Example 4 : Every integer is a rational number. ( True or False )
This is true because every integer can be written as a fraction with a denominator of [latex]1[/latex].
Example 5 : Every natural number is a whole number, integer, and a rational number. ( True or False )
Reviewing the descriptions above, natural numbers are found within the sets of whole numbers, integers, and rational numbers. That makes it a true statement.
We can also use the diagram of funnels above to help us answer this question. If we pour water into the “funnel of natural numbers”, the water should also flow through all the funnels below it. Thus, passing through the funnels of the whole numbers, integers, and rational numbers.
Example 6 : Every whole number is a natural number, integer, and rational number. ( True or False )
Using the same “funnel” analogy; if we pour some liquid into the whole numbers’ funnel, it should pass through the funnels of integers and rational numbers as it makes its way down. Since the natural numbers’ funnel is above the set of whole numbers where we started, we cannot include this funnel in the group.
It is a false statement since whole numbers belong to the sets of integers and rational numbers, but not to the set of natural numbers.
Simply put, the number zero (0) is a counterexample since it is a whole number but not a natural number. So indeed, this is a false statement.
Example 7 : Classify the number zero, [latex]0[/latex].
Definitely not a natural number but it is a whole , an integer , a rational , and a real number. It may not be obvious that zero is also a rational number. However, writing it as a fraction with a nonzero denominator would clearly show that it is indeed a rational number.
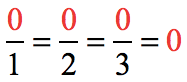
Example 8 : Classify the number [latex]5[/latex].
This is a natural or counting number, a whole number, and an integer. Since we can write it as a fraction with a denominator of [latex]1[/latex], that is, [latex]\Large{5 \over 1}[/latex], it is also a rational number. And of course, this is a real number.
Example 9 : Classify the number [latex]0.25[/latex].
The given decimal number terminates and so we can write it as a fraction which is a characteristic of a rational number. This number is also a real number.
[latex]\Large{0.25 = {{25} \over {100}} = {1 \over 4}}[/latex]
Example 10 : Classify the number [latex]{\rm{2}}{1 \over 5}[/latex].
We can rewrite this mixed fraction as an improper fraction so that it is clear that we have a ratio of two integers.
[latex]\Large{{\rm{2}}{1 \over 5} = {{11} \over 5}}[/latex]
This number is a rational and real number.
Example 11 : Classify the number [latex]{\rm{5.241879132…}}[/latex].
The decimal number is non-terminating and non-repeating that means it is an irrational number. Of course, any irrational number is also a real number.
Example 12 : Classify the number [latex]1.7777…[/latex]
Since the decimal is repeating, it is a rational number. Any rational number must also be a real number.
Example 13 : Classify the number [latex]\sqrt 2 [/latex].
This is an irrational number because when written in decimal form, it is non-terminating and non-repeating. This is also a real number.
Example 14 : Classify the number [latex] – \sqrt {16} [/latex] .
First, we need to simplify this radical expression which gives us [latex] – \sqrt {16} = – \,4[/latex]. The number [latex] – \,4[/latex] is an integer, a rational number, and a real number.
Example 15 : Classify the number [latex] – 8.123123…[/latex].
The decimal number is nonterminating, however, the string of numbers 123 after the decimal point keeps on repeating. We can rewrite the decimal number with a “bar” on top of the repeating numbers.
This makes it a rational number. Don’t forget that it is also a real number.
Take a quiz:
- Classifying Real Numbers Quiz
You might also like these tutorials:
- Properties of Real Numbers
- Properties of Equality
- Math Article
Real Numbers

Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number . Some of the examples of real numbers are 23, -12, 6.99, 5/2, π, and so on. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of real numbers with complete explanations.

Table of contents:
- Set of real numbers
- Commutative
- Associative
- Distributive
Solved Examples
Practice questions, real numbers definition.
Real numbers can be defined as the union of both rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.
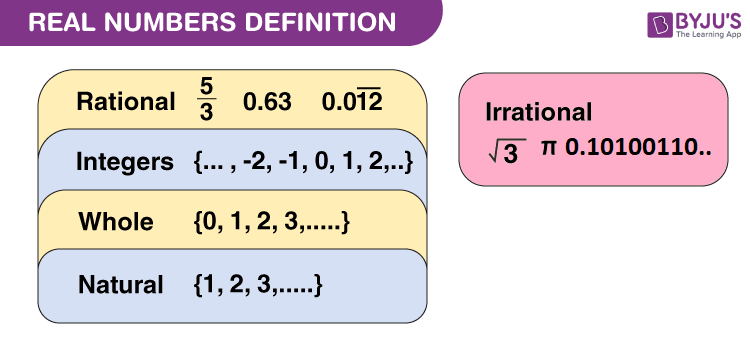
Set of Real Numbers
The set of real numbers consists of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all the real numbers formulas (i.e.) the representation of the classification of real numbers are defined with examples.
| Category | Definition | Example |
|---|---|---|
| Natural Numbers | Contain all counting numbers which start from 1. N = {1, 2, 3, 4,……} | All numbers such as 1, 2, 3, 4, 5, 6,…..… |
| Whole Numbers | Collection of zero and natural numbers. W = {0, 1, 2, 3,…..} | All numbers including 0 such as 0, 1, 2, 3, 4, 5, 6,…..… |
| Integers | The collective result of whole numbers and negative of all natural numbers. | Includes: -infinity (-∞),……..-4, -3, -2, -1, 0, 1, 2, 3, 4, ……+infinity (+∞) |
| Rational Numbers | Numbers that can be written in the form of p/q, where q≠0. | Examples of rational numbers are ½, 5/4 and 12/6 etc. |
| Irrational Numbers | The numbers which are not rational and cannot be written in the form of p/q. | Irrational numbers are non-terminating and non-repeating in nature like √2. |
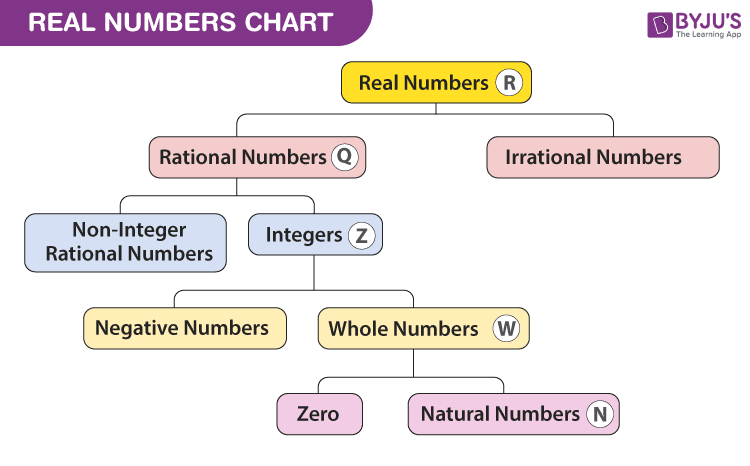
Real Numbers Chart
The chart for the set of real numerals including all the types are given below:
Properties of Real Numbers
The following are the four main properties of real numbers:
- Commutative property
- Associative property
- Distributive property
- Identity property
Consider “m, n and r” are three real numbers. Then the above properties can be described using m, n, and r as shown below:
Commutative Property
If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.
- Addition: m + n = n + m. For example, 5 + 3 = 3 + 5, 2 + 4 = 4 + 2.
- Multiplication: m × n = n × m. For example, 5 × 3 = 3 × 5, 2 × 4 = 4 × 2.
Associative Property
If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.
- Addition: The general form will be m + (n + r) = (m + n) + r. An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.
- Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).
Distributive Property
For three numbers m, n, and r, which are real in nature, the distributive property is represented as:
m (n + r) = mn + mr and (m + n) r = mr + nr.
- Example of distributive property is: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.
Identity Property
There are additive and multiplicative identities.
- For addition: m + 0 = m. (0 is the additive identity)
- For multiplication: m × 1 = 1 × m = m. (1 is the multiplicative identity)
Video Lesson on Numbers

| Learn More About Real Number Properties | |
|---|---|
Find five rational numbers between 1/2 and 3/5.
We shall make the denominator same for both the given rational number
(1 × 5)/(2 × 5) = 5/10 and (3 × 2)/(5 × 2) = 6/10
Now, multiply both the numerator and denominator of both the rational number by 6, we have
(5 × 6)/(10 × 6) = 30/60 and (6 × 6)/(10 × 6) = 36/60
Five rational numbers between 1/2 = 30/60 and 3/5 = 36/60 are
31/60, 32/60, 33/60, 34/60, 35/60.
Write the decimal equivalent of the following:
(i) 1/4 (ii) 5/8 (iii) 3/2
(i) 1/4 = (1 × 25)/(4 × 25) = 25/100 = 0.25
(ii) 5/8 = (5 × 125)/(8 × 125) = 625/1000 = 0.625
(iii) 3/2 = (3 × 5)/(2 × 5) = 15/10 = 1.5
What should be multiplied to 1.25 to get the answer 1?
Solution: 1.25 = 125/100
Now if we multiply this by 100/125, we get
125/100 × 100/125 = 1
- Which is the smallest composite number?
- Prove that any positive odd integer is of the form 6x + 1, 6x + 3, or 6x + 5.
- Evaluate 2 + 3 × 6 – 5.
- What is the product of a non-zero rational number and an irrational number?
Can every positive integer be represented as 4x + 2 (where x is an integer)?
Real Numbers Class 9 and 10
In real numbers Class 9, the common concepts introduced include representing real numbers on a number line, operations on real numbers, properties of real numbers, and the law of exponents for real numbers. In Class 10, some advanced concepts related to real numbers are included. Apart from what are real numbers, students will also learn about the real numbers formulas and concepts such as Euclid’s Division Lemma, Euclid’s Division Algorithm and the fundamental theorem of arithmetic in class 10.
Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.
Frequently Asked Questions on Real Numbers
What are natural and real numbers.
Natural numbers are all positive integers starting from 1 to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, 5, 6, 7, 8, 9, …….∞.
Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.
Is Zero a Real or an Imaginary Number?
Zero is considered to be both a real and an imaginary number. As we know, imaginary numbers are the square root of non-positive real numbers. And since 0 is also a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is defined in a number line and hence a real number.
Are there Real Numbers that are not Rational or Irrational?
No, there are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.
Is the real number a subset of a complex number?
Yes, because a complex number is the combination of a real and imaginary number. So, if the complex number is a set then the real and imaginary numbers are the subsets of it.
What are the properties of real numbers?
Is √3 a real number.
Yes, √3 is a real number. We know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we can also say that √3 is a real number.
Is 3i a real number?
No, 3i is not a real number, as it has an imaginary part in it.
What are the different subsets of real numbers?
The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
According to a new mathematical definition, whole numbers are divided into two sets, one of which is the merger of the sequence of prime numbers and numbers zero and one. Three other definitions, deduced from this first, subdivide the set of whole numbers into four classes of numbers with own and unique arithmetic properties. The geometric distribution of these different types of whole numbers, in various closed matrices, is organized into exact value ratios to 3/2 or 1/1.
can u use any real number of ur choice in mathematics
Where is the chat box?
please send explanation of this.
Sir,I want to know more about mathematics.
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
The Real Numbers (Pre-Algebra Curriculum - Unit 1) | All Things Algebra®

- Google Apps™
What educators are saying
Also included in.

Description
This Real Numbers Unit Bundle includes guided notes, homework assignments, three quizzes, a study guide, and a unit test that cover the following topics:
• Integers and Integer Operations
• Absolute Value
• Simplifying Fractions
• Converting Fractions, Decimals, and Percents
• Adding and Subtracting Fractions
• Multiplying and Dividing Fractions
• Exponents
• Zero Exponent and Negative Exponents
• Perfect Squares and Perfect Cubes
• Square Roots and Cube Roots
• Scientific Notation
• Comparing & Ordering Number Forms
• Order of Operations
• Evaluating Expressions
• The Real Number System
• Properties
ADDITIONAL COMPONENTS INCLUDED:
(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice. Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.
(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes; this is the PDF in Google Slides. I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead!
This resource is included in the following bundle(s):
Pre-Algebra Curriculum
More Pre-Algebra Units:
Unit 2 – Algebraic Expressions
Unit 3 – Equations and Inequalities
Unit 4 – Ratios, Proportions, and Percents
Unit 5 – Functions and Linear Representations
Unit 6 – Systems of Equations
Unit 7 – Geometry
Unit 8 – Measurement: Area and Volume
Unit 9 – Probability and Statistics
LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].
COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.
© All Things Algebra (Gina Wilson), 2012-present
Questions & Answers
All things algebra.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think
- Fundamentals NEW
- Biographies
- Compare Countries
- World Atlas
To share with more than one person, separate addresses with a comma
- Privacy Notice
- Terms of Use
- Kindergarten
- Greater Than Less Than
- Measurement
- Multiplication
- Place Value
- Subtraction
- Punctuation
- 1st Grade Reading
- 2nd Grade Reading
- 3rd Grade Reading
- Cursive Writing
- Alphabet Coloring
- Animals Coloring
- Birthday Coloring
- Boys Coloring
- Buildings Coloring
- Cartoons Coloring
- Christmas Coloring
- Country Flag Coloring
- Country Map Coloring
- Disney Coloring
- Fantasy Coloring
- Food Coloring
- Girls Coloring
- Holidays Coloring
- Music Coloring
- Nature Coloring
- New Year Coloring
- People Coloring
- Religious Coloring
- Sports Coloring
- Toys Coloring
- Transportation Coloring
- US Sports Team Coloring
- Valentine Day Coloring
Unit 1 Real Numbers Homework 5
Displaying top 8 worksheets found for - Unit 1 Real Numbers Homework 5 .
Some of the worksheets for this concept are Unit 1 fractions decimals and percents homework, Homework 9 1 rational exponents answers, Real numbers and number operations, Sets of numbers in the real number system, The real number system, Unit 1 basic economic concepts, Name comparing and ordering real numbers work write, Name date period lesson 9 homework practice.
Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.
1. Unit 1: Fractions, Decimals, and Percents HOMEWORK Page ...
2. homework 9 1 rational exponents answers, 3. 1.1 real numbers and number operations, 4. sets of numbers in the real number system, 5. 1.1 the real number system, 6. unit 1: basic economic concepts, 7. name: comparing and ordering real numbers worksheet write ..., 8. name date period lesson 9 homework practice.

IMAGES
VIDEO
COMMENTS
The Number System Identify the sets to which each of the following numbers belongs by marking an "X" in the appropriate boxes.
The Real Number System All the numbers mentioned in this lesson belong to the set of Real numbers. The set of real numbers is denoted by the symbol [latex]mathbb{R}[/latex]. There are five subsets within the set of real numbers. Let's go over each one of them. Five (5) Subsets of Real Numbers 1) The Set of Natural...
Study with Quizlet and memorize flashcards containing terms like lesson 1, which number is equivalent to (1/3)^-4?, which number equals (3/4)^-2? and more.
Study with Quizlet and memorize flashcards containing terms like Real Number System, Integers, Rational Numbers and more.
Study with Quizlet and memorize flashcards containing terms like Real Numbers, Irrational Numbers, Rational Numbers and more.
The opposites of the counting numbers expanded the number system even further. Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.
Our mission is to improve educational access and learning for everyone. OpenStax is part of Rice University, which is a 501 (c) (3) nonprofit. Give today and help us reach more students. Help. OpenStax.
Grade 8 - Module 9 - THE REAL NUMBER SYSTEM. Big Idea. The set of real numbers includes both rational and irrational numbers and each real number value, including square roots and cube roots, can be approximated on the number line in order to compare and estimate the value of expressions. Vocabulary. real numbers, irrational numbers, rational ...
The real number system is by no means the only field. The {} (which are the real numbers that can be written as r = p / q, where p and q are integers and q ≠ 0) also form a field under addition and multiplication. The simplest possible field consists of two elements, which we denote by 0 and 1, with addition defined by 0 + 0 = 1 + 1 = 0, 1 ...
1.1 - The Real Number System, Classifying Real Numbers & Closure. There's nothing trickier than picking the very first topic to cover in all of Algebra 1. So many options, so what goes first? To start the very first unit of Algebra 1 off, I begin by talking about the real number system and how we classify numbers.
The real number line: We can graph real numbers on a number line. For each point on the number line there corresponds exactly one real number, and this number is called the coordinate of that point.
The classifying numbers in the real number system can be an engaging skill! Check out these 4 strategies for teaching the real number system.
A real number line, or simply number line, allows us to visually display real numbers by associating them with unique points on a line. The real number associated with a point is called a coordinate. A point on the real number line that is associated with a coordinate is called its graph.
How to Classify Real Numbers The "stack of funnels" diagram below will help us easily classify any real numbers. But first, we need to describe what kinds of elements are included in each group of numbers. A funnel represents each group or set of numbers. Description of Each Set of Real Numbers Natural numbers (also...
Real Numbers Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex ...
A number is a quantity. A numeral is a symbol of representation. A system of numeration is a set of numerals and a rule for combining them to make numbers. There have been multiple numeration systems used throughout history and in various cultures.
This Real Numbers Unit Bundle includes guided notes, homework assignments, three quizzes, a study guide, and a unit test that cover the following topics:• Integers and Integer Operations• Absolute Value• Simplifying Fractions• Converting Fractions, Decimals, and Percents• Adding and Subtracting Frac...
Worksheets are Unit 1 real number system homework, Lesson 1 classification and real numbers, Algebra 1 name homework 8 the real number system date, Real numbers and number operations, Sets of numbers in the real number system, Properties of real numbers, Suggested formative assessment tasks formative assessment, Sets of real numbers date period.
Real numbers include the positive and negative integers, fractions (or rational numbers), and irrational numbers. Zero is also a real number.
In this section we introduce the number systems that we will work with in the remainder of this text.
Some of the worksheets for this concept are Real numbers and number operations, Homework 1 unit 5 systems of equations inequalities gina, Georgia standards of excellence curriculum frameworks, Sets of numbers in the real number system, Unit 1, Georgia standards of excellence curriculum frameworks, Teksstaar based lessons, Foundations for algebra.
Displaying top 8 worksheets found for - Unit 1 Real Numbers Homework 5. Some of the worksheets for this concept are Unit 1 fractions decimals and percents homework, Homework 9 1 rational exponents answers, Real numbers and number operations, Sets of numbers in the real number system, The real number system, Unit 1 basic economic concepts, Name ...
The Real Number Line In our study of algebra, we will use several collections of numbers. The real number line allows us to visually display the numbers in which we are interested. A line is composed of infinitely many points. To each point we can associate a unique number, and with each number we can associate a particular point. Coordinate The number associated with a point on the number ...
SECTION 1.1 deals with the axioms that define the real numbers, definitions based on them, and some basic properties that follow from them. SECTION 1.2 emphasizes the principle of mathematical induction. SECTION 1.3 introduces basic ideas of set theory in the context of sets of real numbers. In this section we prove two fundamental theorems: the Heine-Borel and Bolzano-Weierstrass theorems.