Your Article Library
Assignment problem in linear programming : introduction and assignment model.
ADVERTISEMENTS:
Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.
In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.

1. Assignment Model :
Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.
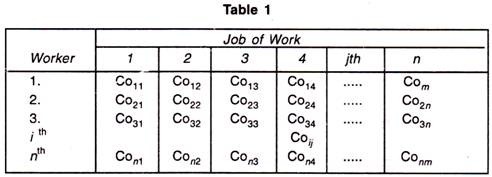
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.
Mathematical Formulation:
Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.
Suppose x jj is a variable which is defined as
1 if the i th job is assigned to j th machine or facility
0 if the i th job is not assigned to j th machine or facility.
Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by
The above definition can be developed into mathematical model as follows:
Determine x ij > 0 (i, j = 1,2, 3…n) in order to
Subjected to constraints

and x ij is either zero or one.
Method to solve Problem (Hungarian Technique):
Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,
1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.
2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.
3. Now, the assignments are made for the reduced table in following manner.
(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.
(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.
(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.
4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:
(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.
(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.
(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.
5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.
6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.
7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.
Related Articles:
- Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
- Linear Programming: Applications, Definitions and Problems
No comments yet.
Leave a reply click here to cancel reply..
You must be logged in to post a comment.
Algorithms: The Assignment Problem
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The “assignment problem” is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world.
Assignment Problem
Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective customers that are requesting service at the same time, and nearby you have multiple drivers that can take them where they need to go. You want to assign the drivers to the customers in a way that minimizes customer wait time (so you keep the customers happy) and driver empty time (so you keep the drivers happy).
The assignment problem is designed for exactly this purpose. We start with m agents and n tasks. We make the rule that every agent has to be assigned to a task. For each agent-task pair, we figure out a cost associated to have that agent perform that task. We then figure out which assignment of agents to tasks minimizes the total cost.
Of course, it may be true that m != n , but that’s OK. If there are too many tasks, we can make up a “dummy” agent that is more expensive than any of the others. This will ensure that the least desirable task will be left to the dummy agent, and we can remove that from the solution. Or, if there are too many agents, we can make up a “dummy” task that is free for any agent. This will ensure that the agent with the highest true cost will get the dummy task, and will be idle.
If that last paragraph was a little dense, don’t worry; there’s an example coming that will help show how it works.
There are special algorithms for solving assignment problems, but one thing that’s nice about them is that a general-purpose solver can handle them too. Below is an example, but first it will help to cover a few concepts that we’ll be using.
Optimization Problems
Up above, we talked about making “rules” and minimizing costs. The usual name for this is optimization. An optimization problem is one where we have an “objective function” (which tells us what our goals are) and one or more “constraint functions” (which tell us what the rules are). The classic example is a factory that can make both “widgets” and “gadgets”. Each “widget” and “gadget” earns a certain amount of profit, but it also uses up raw material and time on the factory’s machines. The optimization problem is to determine exactly how many “widgets” and how many “gadgets” to make to maximize profit (the objective) while fitting within the material and time available (the constraints).
If we were to write this simple optimization problem out, it might look like this:
In this case, we have two variables: g for the number of gadgets we make and w for the number of widgets we make. We also have three constraints that we have to meet. Note that they are inequalities; we might not use all the available material or time in our optimal solution.
Just to unpack this a little: in English, the above is saying that we make 45 dollars / euros / quatloos per gadget we make. However, to make a gadget needs 120 lbs of raw material 1, 80 lbs of raw material 2, and 3.8 hours of machine time. So there is a limit on how many gadgets we can make, and it might be a better use of resources to balance gadgets with widgets.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
Linear Programming
A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.) We can have as many variables as we want, and as many constraint functions as we want, but none of the variables can have exponents in any of the functions. This limitation allows us to apply very efficient mathematical approaches to solve the problem, even for very large problems.
We can state the assignment problem as a linear programming problem. First, we choose to make “i” represent each of our agents (drivers) and “j” to represent each of our tasks (customers). Now, to write a problem like this, we need variables. The best approach is to use “indicator” variables, where xij = 1 means “driver i picks up customer j” and xij = 0 means “driver i does not pick up customer j”.
We wind up with:
This is a compact mathematical way to describe the problem, so again let me put it in English.
First, we need to figure out the cost of having each driver pick up each customer. Then, we can calculate the total cost for any scenario by just adding up the costs for the assignments we pick. For any assignment we don’t pick, xij will equal zero, so that term will just drop out of the sum.
Of course, the way we set up the objective function, the cheapest solution is for no drivers to pick up any customers. That’s not a very good business model. So we need a constraint to show that we want to have a driver assigned to every customer. At the same time, we can’t have a driver assigned to mutiple customers. So we need a constraint for that too. That leads us to the two constraints in the problem. The first just says, if you add up all the assignments for a given driver, you want the total number of assignments for that driver to be exactly one. The second constraint says, if you add up all the assignments to a given customer, you want the total number of drivers assigned to the customer to be one. If you have both of these, then each driver is assigned to exactly one customer, and the customers and drivers are happy. If you do it in a way that minimizes costs, then the business is happy too.
Solving with Octave and GLPK
The GNU Linear Programming Kit is a library that solves exactly these kinds of problems. It’s easy to set up the objective and constraints using GNU Octave and pass these over to GLPK for a solution.
Given some made-up sample data, the program looks like this:
Start with the definition of “c”, the cost information. For this example, I chose to have four drivers and three customers. There are sixteen numbers there; the first four are the cost of each driver to get the first customer, the next four are for the second customer, and the next four are for the third customer. Because we have an extra driver, we add a “dummy” customer at the end that is zero cost. This represents one of the drivers being idle.
The next definition is “b”, the right-hand side of our constraints. There are eight constraints, one for each of the drivers, and one for each of the customers (including the dummy). For each constraint, the right-hand side is 1.
The big block in the middle defines our constraint matrix “a”. This is the most challenging part of taking the mathematical definition and putting it into a form that is usable by GLPK; we have to expand out each constraint. Fortunately, in these kinds of cases, we tend to get pretty patterns that help us know we’re on the right track.
The first line in “a” says that the first customer needs a driver. To see why, remember that in our cost information, the first four numbers are the cost for each driver to get the first customer. With this constraint, we are requiring that one of those four costs be included and therefore that a driver is “selected” for the first customer. The other lines in “a” work similarly; the last four ensure that each driver has an assignment.
Note that the number of rows in “a” matches the number of items in “b”, and the number of columns in “a” matches the number of items in “c”. This is important; GLPK won’t run if this is not true (and our problem isn’t stated right in any case).
Compared to the above, the last few lines are easy.
- “lb” gives the lower bound for each variable.
- “ub” gives the upper bound.
- “ctype” tells GLPK that each constraint is an equality (“strict” as opposed to providing a lower or upper bound).
- “vartype” tells GLPK that these variables are all integers (can’t have half a driver showing up).
- “s” tells GLPK that we want to minimize our costs, not maximize them.
We push all that through a function call to GLPK, and what comes back are two values (along with some other stuff I’ll exclude for clarity):
The first item tells us that our best solution takes 27 minutes, or dollars, or whatever unit we used for cost. The second item tells us the assignments we got. (Note for pedants: I transposed this output to save space.)
This output tells us that customer 1 gets driver 2, customer 2 gets driver 3, customer 3 gets driver 4, and driver 1 is idle. If you look back at the cost data, you can see this makes sense, because driver 1 had some of the most expensive times to the three customers. You can also see that it managed to pick the least expensive pairing for each customer. (Of course, if I had done a better job making up cost data, it might not have picked the least expensive pairing in all cases, because a suboptimal individual pairing might still lead to an overall optimal solution. But this is a toy example.)
Of course, for a real application, we would have to take into consideration many other factors, such as the passage of time. Rather than knowing all of our customers and drivers up front, we would have customers and drivers continually showing up and being assigned. But I hope this simple example has revealed some of the concepts behind optimization and linear programming and the kinds of real-world problems that can be solved.

How to Solve the Assignment Problem: A Complete Guide
Table of Contents
Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.
Understanding the Assignment Problem
Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.
Solving the Assignment Problem
There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.
Step 1: Set up the cost matrix
The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
Step 2: Subtract the smallest element from each row and column
To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.
Step 3: Cover all zeros with the minimum number of lines
The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.
Step 4: Test for optimality and adjust the matrix
To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.
Step 5: Assign the tasks to the agents
The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.
Solution of the Assignment Problem using the Hungarian Method
The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:
- Subtract the smallest entry in each row from all the entries of the row.
- Subtract the smallest entry in each column from all the entries of the column.
- Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
- Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.
The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.
Applications of the Assignment Problem
The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.
Applications in Computer Science
The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.
Applications in Economics
The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.
Applications in Logistics
The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.
Applications in Management
The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.
Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 5 | 7 | 6 |
| Emp 2 | 6 | 4 | 5 |
| Emp 3 | 8 | 5 | 3 |
The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.
Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
Next, we subtract the smallest entry in each column from all the entries of the column:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
| 0 | 0 | 0 |
We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:
Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:
- Emp 1 to Task 3
- Emp 2 to Task 2
- Emp 3 to Task 1
This assignment results in a total time of 9 units.
I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.
Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.
How useful was this post?
Click on a star to rate it!
Average rating 0 / 5. Vote count: 0
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you! 😔
Let us improve this post!
Tell us how we can improve this post?
Operations Research
1 Operations Research-An Overview
- History of O.R.
- Approach, Techniques and Tools
- Phases and Processes of O.R. Study
- Typical Applications of O.R
- Limitations of Operations Research
- Models in Operations Research
- O.R. in real world
2 Linear Programming: Formulation and Graphical Method
- General formulation of Linear Programming Problem
- Optimisation Models
- Basics of Graphic Method
- Important steps to draw graph
- Multiple, Unbounded Solution and Infeasible Problems
- Solving Linear Programming Graphically Using Computer
- Application of Linear Programming in Business and Industry
3 Linear Programming-Simplex Method
- Principle of Simplex Method
- Computational aspect of Simplex Method
- Simplex Method with several Decision Variables
- Two Phase and M-method
- Multiple Solution, Unbounded Solution and Infeasible Problem
- Sensitivity Analysis
- Dual Linear Programming Problem
4 Transportation Problem
- Basic Feasible Solution of a Transportation Problem
- Modified Distribution Method
- Stepping Stone Method
- Unbalanced Transportation Problem
- Degenerate Transportation Problem
- Transhipment Problem
- Maximisation in a Transportation Problem
5 Assignment Problem
- Solution of the Assignment Problem
- Unbalanced Assignment Problem
- Problem with some Infeasible Assignments
- Maximisation in an Assignment Problem
- Crew Assignment Problem
6 Application of Excel Solver to Solve LPP
- Building Excel model for solving LP: An Illustrative Example
7 Goal Programming
- Concepts of goal programming
- Goal programming model formulation
- Graphical method of goal programming
- The simplex method of goal programming
- Using Excel Solver to Solve Goal Programming Models
- Application areas of goal programming
8 Integer Programming
- Some Integer Programming Formulation Techniques
- Binary Representation of General Integer Variables
- Unimodularity
- Cutting Plane Method
- Branch and Bound Method
- Solver Solution
9 Dynamic Programming
- Dynamic Programming Methodology: An Example
- Definitions and Notations
- Dynamic Programming Applications
10 Non-Linear Programming
- Solution of a Non-linear Programming Problem
- Convex and Concave Functions
- Kuhn-Tucker Conditions for Constrained Optimisation
- Quadratic Programming
- Separable Programming
- NLP Models with Solver
11 Introduction to game theory and its Applications
- Important terms in Game Theory
- Saddle points
- Mixed strategies: Games without saddle points
- 2 x n games
- Exploiting an opponent’s mistakes
12 Monte Carlo Simulation
- Reasons for using simulation
- Monte Carlo simulation
- Limitations of simulation
- Steps in the simulation process
- Some practical applications of simulation
- Two typical examples of hand-computed simulation
- Computer simulation
13 Queueing Models
- Characteristics of a queueing model
- Notations and Symbols
- Statistical methods in queueing
- The M/M/I System
- The M/M/C System
- The M/Ek/I System
- Decision problems in queueing
Assignment Problem: Linear Programming
The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.
In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.
The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.
It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.
"A mathematician is a device for turning coffee into theorems." -Paul Erdos
Formulation of an assignment problem
Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:
The structure of an assignment problem is identical to that of a transportation problem.
To formulate the assignment problem in mathematical programming terms , we define the activity variables as
| x = | 1 if job j is performed by worker i | |
| 0 otherwise |
for i = 1, 2, ..., n and j = 1, 2, ..., n
In the above table, c ij is the cost of performing jth job by ith worker.
Generalized Form of an Assignment Problem
The optimization model is
Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn
subject to x i1 + x i2 +..........+ x in = 1 i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1 j = 1, 2,......., n
x ij = 0 or 1
In Σ Sigma notation
x ij = 0 or 1 for all i and j
An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.
Assumptions in Assignment Problem
- Number of jobs is equal to the number of machines or persons.
- Each man or machine is assigned only one job.
- Each man or machine is independently capable of handling any job to be done.
- Assigning criteria is clearly specified (minimizing cost or maximizing profit).
Share this article with your friends
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Assignment Problem
- Feb 20, 2024
The assignment problem is a special case of transportation problem.
Suppose there are $n$ jobs to be performed and $n$ persons are available for these jobs. Assume that each person can do each job at a time, though with varying degree of efficiency.
Let $c_{ij}$ be the cost if the $i^{th}$ person is assigned the $j^{th}$ job. Then the problem is to find an assignment so that the total cost of performing all jobs is minimum. (i.e., which job should be assigned to which person with minimum cost). Such problem is called an Assignment Problem (AP).
The tabular form of the assignment problem is as follows
| Persons \ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
|---|---|---|---|---|---|---|
| Persons/ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
| $1$ | $c_{11}$ | $c_{12}$ | $\cdots$ | $c_{1j}$ | $\cdots$ | $c_{1n}$ |
| $2$ | $c_{21}$ | $c_{22}$ | $\cdots$ | $c_{2j}$ | $\cdots$ | $c_{2n}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $i$ | $c_{i1}$ | $c_{i2}$ | $\cdots$ | $c_{ij}$ | $\cdots$ | $c_{in}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $n$ | $c_{n1}$ | $c_{n2}$ | $\cdots$ | $c_{nj}$ | $\cdots$ | $c_{nn}$ |
The above table is called the $n\times n$ cost-matrix, where $c_{ij}$ are real numbers.
Thus the objective in the Assignment Problem is to assign a number of jobs to the equal number of persons at a minimum cost or maximum profit. e.g. assigning men to offices, classes to rooms, drivers to trucks, problems to research teams etc.
Mathematical Formulation of AP
Mathematically, the AP can be stated as $$ \begin{equation}\label{eq2.4} \min z = \sum_{i=1}^n\sum_{j=1}^n x_{ij} c_{ij}. \end{equation} $$ subject to $$ \begin{equation}\label{eq2.5} \sum_{j=1}^n x_{ij} =1,; \text{ for } i=1,2,\ldots, n \end{equation} $$
$$ \begin{equation}\label{eq2.6} \sum_{i=1}^n x_{ij} =1,; \text{ for } j=1,2,\ldots,n \end{equation} $$ where $$ \begin{equation*} x_{ij}=\left{ \begin{array}{ll} 1, & \hbox{if $i^{th}$ person is assigned $j^{th}$ job;} \ 0, & \hbox{otherwise.} \end{array} \right. \end{equation*} $$ Constraint \eqref{eq2.5} indicate that one job is done by $i^{th}$ person $i=1,2,\ldots, n$ and constraint \eqref{eq2.6} indicate that one person should be assigned $j^{th}$ job $j=1,2,\ldots, n$.
It may be observed from the above formulation that AP is a special type of Linear programming problem.
Unbalanced Assignment Problem
If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem . In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
Maximal Assignment Problem
Sometimes, the assignment problem deals with the maximization of an objective function instead of minimization.. For example, it may be required to assign persons to jobs in such a way that the expected profit is maximum. In such a case, first convert the problem of maximization to minimization and apply the usual procedure of assignment.
The assignment problem of maximization type can be converted to minimization type by subtracting all the elements of the given profit matrix from the largest element.
Restrictions on Assignment
Sometimes due to technical or other difficulties do not permit the assignment of a particular facility to a particular job. In such a situation, the difficulty can be overcome by assigning a very high cost (say, infinity i.e. $\infty$) to the corresponding cell.
Because of assigning an infinite penalty to such a cell the activity will be automatically excluded from the optimal solution. Then apply the usual procedure to find the optimal assignment.

- Linear Programming Problem and Its Mathematical Formulation
Sometimes one seeks to optimize (maximize or minimize) a known function (could be profit/loss or any output), subject to a set of linear constraints on the function. Linear Programming Problems (LPP) provide the method of finding such an optimized function along with/or the values which would optimize the required function accordingly.
Browse more Topics under Linear Programming
- Different Types of Linear Programming Problems
- Graphical Method of Solving Linear Programming Problems
It is one of the most important Operations Research tools. It is widely used as a decision making aid in almost all industries. There can be various fields of application of LPP, in the areas of Economics, Computer Sciences, Mathematics , etc. Since it is a very important topic with numerous practical applications , we will proceed slowly in building up this topic and making it very clear to you. So, let’s begin!
Suggested Videos on Linear Programming
.embed-container { position: relative; padding-bottom: 56.25%; height: 0; overflow: hidden; max-width: 100%; } .embed-container iframe, .embed-container object, .embed-container embed { position: absolute; top: 0; left: 0; width: 100%; height: 100%; }
Mathematical Formulation
Formulation of an LPP refers to translating the real-world problem into the form of mathematical equations which could be solved. It usually requires a thorough understanding of the problem.


Steps towards formulating a Linear Programming problem:
- Step 1: Identify the ‘n’ number of decision variables which govern the behaviour of the objective function (which needs to be optimized).
- Step 2: Identify the set of constraints on the decision variables and express them in the form of linear equations / inequations . This will set up our region in the n- dimensional space within which the objective function needs to be optimized. Don’t forget to impose the condition of non-negativity on the decision variables i.e. all of them must be positive since the problem might represent a physical scenario, and such variables can’t be negative.
- Step 3: Express the objective function in the form of a linear equation in the decision variables.
- Step 4: Optimize the objective function either graphically or mathematically.
Now let us look at an example aimed at enabling you to learn how to formulate a problem in Linear Programming!
Download Linear Programming Problem Cheat Sheet

Solved Examples for You
Question 1: A calculator company produces a handheld calculator and a scientific calculator. Long-term projections indicate an expected demand of at least 150 scientific and 100 handheld calculators each day. Because of limitations on production capacity, no more than 250 scientific and 200 handheld calculators can be made daily.
To satisfy a shipping contract, a minimum of 250 calculators must be shipped each day. If each scientific calculator sold, results in a 20 rupees loss, but each handheld calculator produces a 50 rupees profit; then how many of each type should be manufactured daily to maximize the net profit?
Such word problems can be very tricky to solve if not formulated properly. Hence, let us approach it in a step by step manner as discussed above.
Step 1: The decision variables : Since the question has asked for an optimum number of calculators, that’s what our decision variables in this problem would be. Let,
x = number of scientific calculators produced y = number of handheld calculators produced
Therefore, we have 2 decision variables in this problem, namely ‘ x’ and ‘ y’.
Step 2: The constraints: Since the company can’t produce a negative number of calculators in a day, a natural constraint would be:
x ≥ 0 y ≥ 0
However, a lower bound for the company to sell calculators is already supplied in the problem. We can note it down as:
x ≥ 150 y ≥ 100
We have also been given an upper bound for these variables, owing to the limitations on production by the company. We can write as follows:
x ≤ 250 y ≤ 200
Besides, we also have a joint constraint on the values of ‘x’ and ‘y’ due to the minimum order on a shipping consignment; given as:
x + y ≥ 250
Step 3: Objective Function: Clearly, here we need to optimize the Net Profit function. The Net Profit Function is given as:
P = -20x + 50y
Step 4: Solving the problem: the system here –
Maximization of P = -20x + 50y, subject to: 150 ≤ x ≤ 250 100 ≤ y ≤ 200 x + y ≥ 250
We can solve it graphically or mathematically as per convenience. We will discuss it in later sections. This completes the discussion on the mathematical formulation of a Linear Programming problem !
Question 2: What is meant by LPP?
Answer: The full form of LPP is Linear Programming Problems. This method helps in achieving the best outcome in a mathematical model. The best outcome could be maximum profit or the lowest cost or the best possible price. The representation of this model’s requirements is by linear relationships.
Question 3: Explain how one can calculate LPP?
Answer: In order to calculate LPP, one must follow the following steps:
- Formulate the LP problem.
- Construct a graph and then plot the various constraint lines.
- Ascertain the valid side of all constraint lines.
- Identify the region of feasible solution.
- Plot the objective function.
- Finally, find out the optimum point.
Question 4: What are the various advantages of LPP?
Answer: The various advantages of LPP are as follows:
- Utilized for analyzing numerous military, social, economic social, and industrial problems.
- Linear programming is appropriate for solving complex problems.
- It assists in productive management of an organization for better outcomes.
Question 5: Who is credited with the development of LPP?
Customize your course in 30 seconds
Which class are you in.

Linear Programming
- Types of Linear Programming Problems
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Download the App

- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Integration Formulas
- Differentiation Formulas
- Trigonometry Formulas
- Algebra Formulas
- Mensuration Formula
- Statistics Formulas
- Trigonometric Table
Linear Programming
Linear programming is a mathematical concept that is used to find the optimal solution of the linear function. This method uses simple assumptions for optimizing the given function. Linear Programming has a huge real-world application and it is used to solve various types of problems.
The term “linear programming” consists of two words linear and programming, the word linear tells the relation between various types of variables of degree one used in a problem and the word programming tells us the step-by-step procedure to solve these problems.
In this article, we will learn about linear programming, its examples, formulas, and other concepts in detail.
Table of Content
What is Linear Programming?
Components of linear programming, linear programming examples, linear programming problems, types of linear programming problems, linear programming formula, how to solve linear programming problems, linear programming methods, linear programming simplex method, linear programming graphical method, linear programming applications, importance of linear programming, up-to-date applications of linear programming, linear programming in operations research, simplex method.
Linear programming or Linear optimization is a technique that helps us to find the optimum solution for a given problem, an optimum solution is a solution that is the best possible outcome of a given particular problem.
In simple terms, it is the method to find out how to do something in the best possible way. With limited resources, you need to do the optimum utilization of resources and achieve the best possible result in a particular objective such as least cost, highest margin, or least time.
The situation that requires a search for the best values of the variables subject to certain constraints is where we use linear programming problems. These situations cannot be handled by the usual calculus and numerical techniques.
Linear Programming Definition
Linear programming is the technique used for optimizing a particular scenario. Using linear programming provides us with the best possible outcome in a given situation. It uses all the available resources in a manner such that they produce the optimum result.
The basic components of a linear programming(LP) problem are:
- Decision Variables: Variables you want to determine to achieve the optimal solution.
- Objective Function: M athematical equation that represents the goal you want to achieve
- Constraints: Limitations or restrictions that your decision variables must follow.
- Non-Negativity Restrictions: In some real-world scenarios, decision variables cannot be negative
Additional Characteristics of Linear Programming
- Finiteness: The number of decision variables and constraints in an LP problem are finite.
- Linearity: The objective function and all constraints must be linear functions of the decision variables . It means the degree of variables should be one.
We can understand the situations in which Linear programming is applied with the help of the example discussed below,
Suppose a delivery man has to deliver 8 packets in a day to the different locations of a city. He has to pick all the packets from A and has to deliver them to points P, Q, R, S, T, U, V, and W. The distance between them is indicated using the lines as shown in the image below. The shortest path followed by the delivery man is calculated using the concept of Linear Programming.
Linear Programming Problems (LPP) involve optimizing a linear function to find the optimal value solution for the function. The optimal value can be either the maximum value or the minimum value.
In LPP, the linear functions are called objective functions. An objective function can have multiple variables, which are subjected to conditions and have to satisfy the linear constraints .
There are many different linear programming problems(LPP) but we will deal with three major linear programming problems in this article.
Manufacturing Problems
Manufacturing problems are a problem that deals with the number of units that should be produced or sold to maximize profits when each product requires fixed manpower, machine hours, and raw materials.
Diet Problems
It is used to calculate the number of different kinds of constituents to be included in the diet to get the minimum cost, subject to the availability of food and their prices.
Transportation Problems
It is used to determine the transportation schedule to find the cheapest way of transporting a product from plants /factories situated at different locations to different markets.
A linear programming problem consists of,
- Decision variables
- Objective function
- Constraints
- Non-Negative restrictions
Decision variables are the variables x, and y, which decide the output of the linear programming problem and represent the final solution.
The objective function , generally represented by Z, is the linear function that needs to be optimized according to the given condition to get the final solution.
The restrictions imposed on decision variables that limit their values are called constraints.
Now, the general formula of a linear programming problem is,
Objective Function : Z = ax + by
Constraints: cx + dy ≥ e, px + qy ≤ r
Non-Negative restrictions: x ≥ 0, y ≥ 0
In the above condition x, and y are the decision variables.
Before solving the linear programming problems first we have to formulate the problems according to the standard parameters. The steps for solving linear programming problems are,
Step 1: Mark the decision variables in the problem. Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized. Step 3: Write down all the constraints of the linear problems. Step 4: Ensure non-negative restrictions of the decision variables. Step 5: Now solve the linear programming problem using any method generally we use either the simplex or graphical method.
We use various methods for solving linear programming problems. The two most common methods used are,
- Graphical Method
Let’s learn about these two methods in detail in this article,
One of the most common methods to solve the linear programming problem is the simplex method. In this method, we repeat a specific condition ‘n’ a number of times until an optimum solution is achieved.
The steps required to solve linear programming problems using the simplex method are,
Step 1: Formulate the linear programming problems based on the given constraints. Step 2: Convert all the given inequalities to equations or equalities of the linear programming problems by adding the slack variable to each inequality where ever required. Step 3: Construct the initial simplex table. By representing each constraint equation in a row and writing the objective function at the bottom row. The table so obtained is called the Simplex table. Step 4: Identify the greatest negative entry in the bottom row the column of the element with the highest negative entry is called the pivot column Step 5: Divide the entries of the right-most column with the entries of the respective pivot column, excluding the entries of the bottommost row. Now the row containing the least entry is called the pivot row. The pivot element is obtained by the intersection of the pivot row and the pivot column. Step 6: Using matrix operation and with the help of the pivot element make all the entries in the pivot column to be zero. Step 7: Check for the non-negative entries in the bottommost row if there are no negative entries in the bottom row, end the process else start the process again from step 4. Step 8: The final simplex table so obtained gives the solution to our problem.
Graphical Method is another method than the Simplex method which is used to solve linear programming problems. As the name suggests this method uses graphs to solve the given linear programming problems. This is the best method to solve linear programming problems and requires less effort than the simplex method.
While using this method we plot all the inequalities that are subjected to constraints in the given linear programming problems. As soon as all the inequalities of the given LPP are plotted in the XY graph the common region of all the inequalities gives the optimum solution. All the corner points of the feasible region are calculated and the value of the objective function at all those points is calculated then comparing these values we get the optimum solution of the LPP.
Example: Find the maximal and minimal value of z = 6x + 9y when the constraint conditions are,
- 2x + 3y ≤ 12
- x and y ≥ 0
Step 1 : First convert the inequations into normal equations. Hence the equations will be 2x+3y = 0, x = 0, y = 0 and x + y = 5. Step 2 : Find the points at which 2x + 3y and x + y = 5 cut the x-axis and y-axis. To find the point of intersection of the x-axis put y = 0 in the respective equation and find the point. Similarly for y-axis intersection points put x = 0 in the respective equation. Step 3 : Draw the two lines cutting the x-axis and y-axis. We find that the two axes cut each other at (3,2). Step 4 : For x ≥ 0 and y ≥ 0, we find that both inequations are followed. Hence the region will include an area region enclosed by two axes and both lines including the origin. The plotted region is shown below in the figure. Step 5 : Find Z for each point and maxima and minima. Coordinates Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Hence, we find that Z = 6x + 9y is maximum at (0,5) and minimum at (5,0).
Linear Programming has applications in various fields. It is used to find the minimum cost of a process when all the constraints of the problems are given. It is used to optimize the transportation cost of the vehicle, etc. Various applications of Linear Programming are
Engineering Industries
Engineering Industries use linear programming to solve design and manufacturing problems and to get the maximum output from a given condition.
Manufacturing Industries
Manufacturing Industries use linear programming to maximize the profit of the companies and to reduce the manufacturing cost.
Energy Industries
Energy companies use linear programming to optimize their production output.
Transportation Industries
Linear programming is also used in transportation industries to find the path to minimize the cost of transportation.
Linear Programming has huge importance in various industries it maximizes the output value while minimizing the input values according to various constraints.
LP is highly applicable when we have multiple conditions while solving a problem and we have to optimize the output of the problem i.e. either we have to find the minimum or the maximum value according to a given condition.
Linear Inequalities Algebraic Solution of Linear Inequalities
Problem 1: A company manufactures and sells two types of products and the cost of production of each unit a and b is rupees 200 and 150 respectively each unit of product yields a profit of 20 rupees and each unit of product b yields a profit of 15 rupees on selling. The company estimates the monthly demand of A and B to be at a maximum of the harvested unit in all the production budget for the month is set at rupees 50000. How many units should the company manufacture to earn maximum profit from its monthly sales from a and b?
Let x = number of units of type A y = Number of units of type B Maximize Z = 40x + 50y Subject to the constraints 3x + y ≤ 9 x + 2y ≤ 8 and x, y ≥ 0 Consider the equation, 3x + y = 9 x = 3 y = 0 and x + 2y = 8 x = 8 y = 0 Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) is shown below Vertices Z = 40x + 50y (0, 0) Z = 40 × 0 + 50 × 0 = Rs. 0 (3, 0) Z = 40 × 3 + 50 × 0 = Rs. 120 (0, 4) Z = 40 × 0 + 50 × 4 = Rs. 200 (2, 3) Z = 40 × 2 + 50 × 3 = Rs. 230 Maximum profit, Z = Rs. 230 ∴ Number of units of type A is 2 and the number of units of type B is 3.
Problem 2: Maximize Z = 3x + 4y.
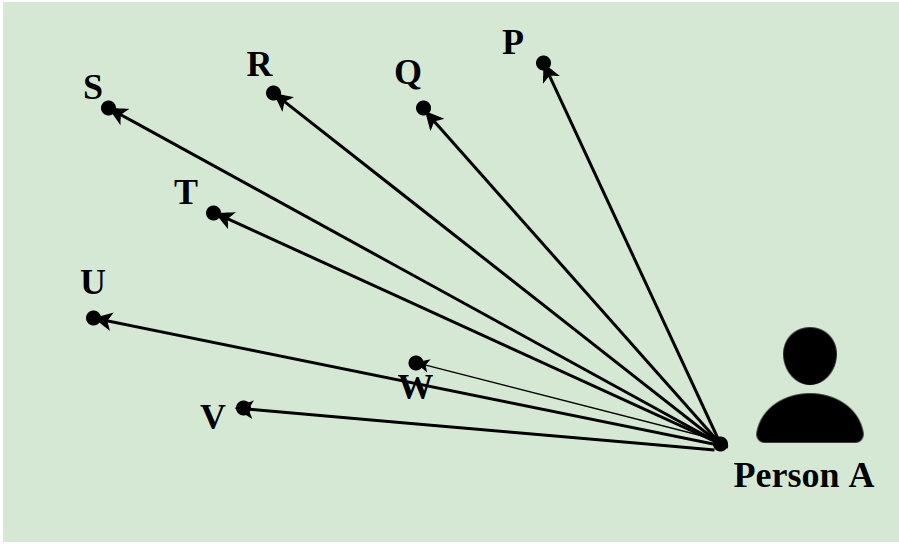
Subject to constraints , x + y ≤ 450, 2x + y ≤ 600 and x, y ≤ 0.
We have from the given Constraints (1) X + Y = 450 Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450 Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450 From, Constraints (2) 2x + y = 600 Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600 Putting y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300 Now, we have the points co-ordinate Z = 3x + 4y
Vertices | Z = 3x + 4y |
|---|---|
(0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
(300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
(150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
(0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Therefore, the optimal solution maximum Z = 1800 at co-ordinate x = 0 and y = 450. The graph is given below.
Linear programming, a powerful mathematical technique, is used to solve optimization problems in various industries. Here are some modern applications:
- Supply Chain Optimization : Linear programming helps companies minimize costs and maximize efficiency in their supply chains. It’s used for determining the most cost-effective transportation routes, warehouse operations, and inventory management strategies.
- Energy Management : In the energy sector, linear programming is utilized to optimize the mix of energy production methods. This includes balancing traditional energy sources with renewable ones to reduce costs and environmental impact while meeting demand.
- Telecommunications Network Design : Linear programming aids in designing efficient telecommunications networks. It helps in allocating bandwidth, designing network layouts, and optimizing the flow of data to ensure high-speed communication at lower costs.
- Financial Planning : Businesses and financial analysts use linear programming for portfolio optimization, risk management, and capital budgeting. It helps in making investment decisions that maximize returns while minimizing risk.
- Healthcare Logistics : In healthcare, linear programming is applied to optimize the allocation of resources, such as hospital beds, medical staff, and equipment. It’s crucial for improving patient care, reducing wait times, and managing costs effectively.
- Manufacturing Process Optimization : Linear programming is used to determine the optimal production levels for multiple products within a manufacturing facility, considering constraints like labor, materials, and machine availability.
- Agricultural Planning : Farmers and agricultural planners use linear programming to decide on crop selection, land use, and resource allocation to maximize yields and profits while conserving resources.
- Airline Crew Scheduling : Airlines employ linear programming to schedule crews efficiently, ensuring that flights are staffed in compliance with regulations and minimizing operational costs.
These applications demonstrate the versatility and power of linear programming in solving complex optimization problems across various sectors, showcasing its relevance in today’s data-driven world.
- Core Tool : Linear programming is a foundational tool in operations research for optimizing resources.
- Decision Making : Helps in making the best decisions regarding resource allocation, maximizing profits, or minimizing costs.
- Wide Applications : Used in various fields such as logistics, manufacturing, finance, and healthcare for solving complex problems.
- Modeling Real-World Problems : Transforms real-world problems into mathematical models to find the most efficient solutions.
- Optimization Algorithm : The Simplex Method is a powerful algorithm used in linear programming to find the optimal solution to linear inequalities.
- Step-by-Step Approach : It iteratively moves towards the best solution by navigating the edges of the feasible region defined by constraints.
- Efficiency : Known for its efficiency in solving large-scale linear programming problems.
- Versatility : Applicable in various domains like diet planning, network flows, production scheduling, and more, showcasing its versatility.
Practice Problems on Linear Programming
Problem 1: Maximize Z=3x+4y subject to the constraints:
- [Tex]x+2\leq 8[/Tex]
- [Tex]3x+y\leq 9[/Tex]
- [Tex]x \geq 0[/Tex]
- [Tex]y \geq 0[/Tex]
Problem 2: Minimize Z=5x+2y subject to the constraints:
- [Tex]2x + y \geq 10[/Tex]
- [Tex]x + 3y \geq 15[/Tex]
Problem 3: A factory produces two products, P1 and P2. The profit for P1 is $40 and for P2 is $30. Each product requires processing in two departments. The processing times in hours per unit for each department are given below:
| Product | Department A | Department B |
|---|---|---|
| P1 | 2 | 1 |
| P2 | 1 | 2 |
The available hours for Department A are 100 and for Department B are 80. Formulate the linear programming problem to maximize the profit.
Problem 4: Minimize the cost of a diet containing at least 60 units of protein and 70 units of carbohydrates. Two food items, A and B, provide the following nutrients per unit:
| Nutrient | Food A | Food B |
|---|---|---|
| Protein | 3 | 4 |
| Carbohydrates | 4 | 2 |
The cost per unit of food A is $2 and food B is $3. Formulate the linear programming problem to minimize the cost.
Problem 5: A company needs to transport goods from two warehouses to three retail stores. The supply at Warehouse 1 is 70 units, and at Warehouse 2 is 80 units. The demand at Store 1 is 40 units, at Store 2 is 50 units, and at Store 3 is 60 units. The transportation costs per unit are given below:
| Store 1 | Store 2 | Store 3 | |
|---|---|---|---|
| Warehouse 1 | $4 | $6 | $8 |
| Warehouse 2 | $5 | $3 | $7 |
Formulate the linear programming problem to minimize the transportation cost.
Problem 6: Maximize the return on an investment portfolio consisting of two investments, A and B. Investment A has a return of 5% and investment B has a return of 7%. The total investment is $100,000, with at least $30,000 in investment A and no more than $60,000 in investment B. Formulate the linear programming problem.
Problem 7: A company needs to schedule workers for a week with the following constraints: At least 3 workers on Monday, 2 on Tuesday, 4 on Wednesday, 3 on Thursday, and 5 on Friday. Each worker can work at most 3 days a week. Formulate the linear programming problem to minimize the number of workers needed.
Problem 8: A company produces a blend of two chemicals, A and B. The blend must contain at least 30% of A and at least 40% of B. Chemical A costs $10 per unit and chemical B costs $15 per unit. The company needs to produce 100 units of the blend. Formulate the linear programming problem to minimize the cost.
Problem 9: Assign 4 workers to 4 jobs with the following costs:
| Job 1 | Job 2 | Job 3 | Job 4 | |
|---|---|---|---|---|
| Worker 1 | $9 | $2 | $7 | $8 |
| Worker 2 | $6 | $4 | $3 | $7 |
| Worker 3 | $5 | $8 | $1 | $8 |
| Worker 4 | $7 | $6 | $9 | $4 |
Formulate the linear programming problem to minimize the total cost.
Problem 10: An investor wants to maximize the return from a portfolio consisting of three investments: X, Y, and Z. The returns are 6%, 8%, and 10%, respectively. The total investment is $200,000, with at least $50,000 in each investment and at least as much in X as in Y. Formulate the linear programming problem.
Linear Programming – FAQs
What is linear programming.
Linear programming is a mathematical concept which is used to optimize a given linear problem which has a variety of constraints. Using linear programming we the optimum output of the given problem
What are Linear Programming Problems?
Linear Programming Problems (LPP) are the problems which give the optimum solution to the given conditions.
What is Linear Programming Formula?
General Linear Programming Formulas are, Objective Function: Z = ax + by Constraints: px + qy ≤ r, sx + ty ≤ u Non-Negative Restrictions: x ≥ 0, y ≥ 0
What are the different types of Linear Programming?
Different types of linear programming methods are, Linear Programming by Simplex Method Linear Programming by R Method Linear Programming by Graphical Method
What are requirements of Linear Programming?
Various requirements of linear programming problems are, Linearity Objective Function Constraints Non-negativity
What are the advantages of Linear Programming?
Various advantages of linear programming are, It provides the optimal solution to any given linear problem. It is easy to use and always gives consistent results It helps to maximize profits and to reduce the input cost.
Please Login to comment...
Similar reads.
- School Learning
- Technical Scripter
- Math-Concepts
- Maths-Class-12
- Technical Scripter 2020
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- Math Article
- Linear Programming Problem Lpp
Linear programming problem (LPP)

Linear Programming Problems (LPP): Linear programming or linear optimization is a process which takes into consideration certain linear relationships to obtain the best possible solution to a mathematical model. It is also denoted as LPP. It includes problems dealing with maximizing profits, minimizing costs, minimal usage of resources, etc. These problems can be solved through the simplex method or graphical method.
The Linear programming applications are present in broad disciplines such as commerce, industry, etc. In this section, we will discuss, how to do the mathematical formulation of the LPP.
Mathematical Formulation of Problem
Let x and y be the number of cabinets of types 1 and 2 respectively that he must manufacture. They are non-negative and known as non-negative constraints.
The company can invest a total of 540 hours of the labour force and is required to create up to 50 cabinets. Hence,
15x + 9y <= 540
x + y <= 50
The above two equations are known as linear constraints.
Let Z be the profit he earns from manufacturing x and y pieces of the cabinets of types 1 and 2. Thus,
Z = 5000x + 3000y
Our objective here is to maximize Z. Hence Z is known as the objective function. To find the answer to this question, we use graphs, which is known as the graphical method of solving LPP. We will cover this in the subsequent sections.
Graphical Method
The solution for problems based on linear programming is determined with the help of the feasible region, in case of graphical method. The feasible region is basically the common region determined by all constraints including non-negative constraints, say, x,y≥0, of an LPP. Each point in this feasible region represents the feasible solution of the constraints and therefore, is called the solution/feasible region for the problem. The region apart from (outside) the feasible region is called as the infeasible region .
The optimal value (maximum and minimum) obtained of an objective function in the feasible region at any point is called an optimal solution. To learn the graphical method to solve linear programming completely reach us.
Linear Programming Applications
Let us take a real-life problem to understand linear programming. A home décor company received an order to manufacture cabinets. The first consignment requires up to 50 cabinets. There are two types of cabinets. The first type requires 15 hours of the labour force (per piece) to be constructed and gives a profit of Rs 5000 per piece to the company. Whereas, the second type requires 9 hours of the labour force and makes a profit of Rs 3000 per piece. However, the company has only 540 hours of workforce available for the manufacture of the cabinets. With this information given, you are required to find a deal which gives the maximum profit to the décor company.

Given the situation, let us take up different scenarios to analyse how the profit can be maximized.
- He decides to construct all the cabinets of the first type. In this case, he can create 540/15 = 36 cabinets. This would give him a profit of Rs 5000 × 36 = Rs 180,000.
- He decides to construct all the cabinets of the second type. In this case, he can create 540/9 = 60 cabinets. But the first consignment requires only up to 50 cabinets. Hence, he can make profit of Rs 3000 × 50 = Rs 150,000.
- He decides to make 15 cabinets of type 1 and 35 of type 2. In this case, his profit is (5000 × 15 + 3000 × 35) Rs 180,000.
Similarly, there can be many strategies which he can devise to maximize his profit by allocating the different amount of labour force to the two types of cabinets. We do a mathematical formulation of the discussed LPP to find out the strategy which would lead to maximum profit.
Related Links
To learn more about solving LPP, download BYJU’S The Learning App.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

An assignment problem can be solved by
An assignment problem can be solved by.
A. Simplex method
B. Transportation method
C. Both a & b
D. None of the above
Answer: Option C
Solution(By Examveda Team)
This Question Belongs to Management >> Operations Research
Join The Discussion
Related Questions on Operations Research
The use of decision models.
A. Is possible when the variables value is known
B. Reduces the scope of judgement & intuition known with certainty in decision-making
C. Require the use of computer software
Every mathematical model.
A. Must be deterministic
B. Requires computer aid for its solution
C. Represents data in numerical form
D. All of the above
A physical model is example of.
A. An iconic model
B. An analogue model
C. A verbal model
D. A mathematical model
The qualitative approach to decision analysis relies on.
A. Experience
B. Judgement
C. Intuition
More Related Questions on Operations Research
Read More: MCQ Type Questions and Answers
- Arithmetic Ability
- Competitive Reasoning
- Competitive English
- Data Interpretation
- General Knowledge
- State GK
- History
- Geography
- Current Affairs
- Banking Awareness
- Computer Fundamentals
- Networking
- C Program
- Java Program
- Database
- HTML
- Javascript
- Computer Science
- Electronics and Communications Engineering
- Electrical Engineering
- Mechanical Engineering
- Civil Engineering
- Chemical Engineering
- Automobile Engineering
- Biotechnology Engineering
- Mining Engineering
- Commerce
- Management
- Philosophy
- Agriculture
- Sociology
- Political Science
- Pharmacy

IMAGES
COMMENTS
The formal definition of the assignment problem (or linear assignment problem) is . Given two sets, A and T, together with a weight function C : A × T → R.Find a bijection f : A → T such that the cost function: (, ())is minimized. Usually the weight function is viewed as a square real-valued matrix C, so that the cost function is written down as: , The problem is "linear" because the cost ...
t 5 January 18, 2011Lecture 5In which w. gramming.1 Linear ProgrammingA linear program is an optimization problem in which we have a collection of variables, which can take real values, and we want to nd an assignment of values to the variables that satis es a given collection of linear inequalities and that maximizes or min.
Following steps are involved in solving this Assignment problem, 1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.
The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear. Linear Programming. A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.)
In this work, the problem of job-machine assignment was formulated as a linear programming (LP) models and then solved by the simplex method. Three case studies were involved in this study to cover all kinds of problems may be faced. To verify the results of the LP models, these problems also solved using transportation algorithm and has been ...
Formulating Linear Programming Models LP Example #4 (Assignment Problem) The coach of a swim team needs to assign swimmers to a 200-yard medley relay team (four swimmers, each swims 50 yards of one of the four strokes). Since most of the best swimmers are very fast in more than one stroke, it is not clear which
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
Assignment Problem: Linear Programming. The assignment problem is a special type of transportation problem, where the objective is to minimize the cost or time of completing a number of jobs by a number of persons. In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an ...
UNIT -2. r: IIASSIGNMENT PROBLEMIntroduction:Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a. number of jobs by a number of persons. The assignment problem in the general form can be stated as follows: "Given n facilities, n jobs and the effectiveness of ...
e minimisation problem.3. The assignment problem wherein the number of rows is not equal to the number of columns is said t. be an unbalanced problem. Such a problem is handled by introducing dummy row(s) if the number of rows is less than the number of columns and dummy column(s) if the number of columns is le.
Unbalanced Assignment Problem. If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem. In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
Linear programming. er: Michel Goemans1 BasicsLinear Programming deals with the problem of optimizing a linear objective function subject to linear equality and inequality constraint. on the decision variables. Linear programming has many practical applications (in transportation. production planning, ...). It is also the building block for.
problem. Hungarian method is one of them See [1, 2] for the history of this method. Various articles [3, 4, 5, and 6] have been published for solving these type of problem. In this paper we achieved exact optimal solution, which is same as that of Hungarian method. II. FORMATION OF ASSIGNMENT PROBLEM The Assignment problem can be stated in the ...
called the assignment problem. ) We could set up a transportation problem and solve it using the simplex method as with any LP problem (see Using the Simplex Method to Solve Linear Programming Maximization Problems, EM 8720, or another of the sources listed on page 35 for informa-tion about the simplex method). However, the special structure of
Elements of a basic LPP. Decision Variables: These are the unknown quantities that are expected to be estimated as an output of the LPP solution. Objective Function: All linear programming problems aim to either maximize or minimize some numerical value representing profit, cost, production quantity, etc.
Lecture 15: Linear Programming. Linear programming (LP) is a method to achieve the optimum outcome under some requirements represented by linear relationships. More precisely, LP can solve the problem of maximizing or minimizing a linear objective function subject to some linear constraints. In general, the standard form of LP consists of ...
Learning Objectives. In module 3, we discussed about how to represent a Linear Programming (LP) model in various forms and also some of the most popular methods like simplex method to solve a LP problem (LPP). In this module, an introduction to solve a LPP using software will be given. This will help the reader to solve large LPP more easily ...
Steps towards formulating a Linear Programming problem: Step 1: Identify the 'n' number of decision variables which govern the behaviour of the objective function (which needs to be optimized). Step 2: Identify the set of constraints on the decision variables and express them in the form of linear equations / inequations.
Step 1: Mark the decision variables in the problem. Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized. Step 3: Write down all the constraints of the linear problems. Step 4: Ensure non-negative restrictions of the decision variables.
It is also denoted as LPP. It includes problems dealing with maximizing profits, minimizing costs, minimal usage of resources, etc. These problems can be solved through the simplex method or graphical method. The Linear programming applications are present in broad disciplines such as commerce, industry, etc.
Linear Programming Problem, or LPP, is a mathematical method to determine the best possible outcome for a given set of parameters represented in linear relationships. This article will briefly discuss LPP, its definitions, basic terminologies, methods to solve the Linear Programming Problem and its applications.
An assignment problem can be solved by Simplex method and Transportation method. The simplex method is a method for solving problems in linear programming. This method, invented by George Dantzig in 1947, tests adjacent vertices of the feasible set (which is a polytope) in sequence so that at each new vertex the objective function improves or ...